






-->こちらへ<--
このページは当事業所で御提供するデータ解析業務について、これらの計算の内容の簡単なご紹介及びこれらの計算がどのような役に立つのかということをご説明するページです。このページでご紹介している以外の項目については、上の”データ解析”のボタンをクリックして下さい。なお、データ解析業務の項目の一部のご紹介のページは現在構築中ですので、ご不明な点はメール等でお問い合せ頂きますようお願い致します。
このページではデータから計算された平均がどれくらい確かなのかといったようなことについてご説明しています。
母集団、サンプルについて
平均とはある数のデータの総計をそのデータの個数で割ったものということをご存じの方は多いと思います。ただ、実際には個々のデータの値は平均値とは異なるものですが、平均値だけでは、個々のデータの値と平均との値の差が重要なのかどうか、あるいは計算された平均がどの程度確かなのかといったことがわかりません。そこで、このページでは計算された平均がどの程度確かなのか、個々のデータの値と平均との値の差が重要かどうかや、2つのデータ群があった場合にそれらの平均値は異なるといえるかどうかというようなトピックについて簡単に御説明致します。なお、統計では一般に母集団とサンプル(標本)を区別します。具体的には、例えば、20歳代の日本人の平均身長を知りたい場合に、母集団とは20歳代の日本人全員です。しかし、20歳代の日本人全員の身長のデータを得ることは、コストや、手間、また協力を得られるかどうかの点で実現することは不可能と考えられます。そこで、通常は20歳代の日本人全員のうち一部の人達の身長のデータを用いることになりますが、この、実際手に入るデータをサンプルと言い、通常はこのサンプルの値から、母集団、すなわち、20歳代の日本人全員の平均身長を”推定”することになります。
正規分布について
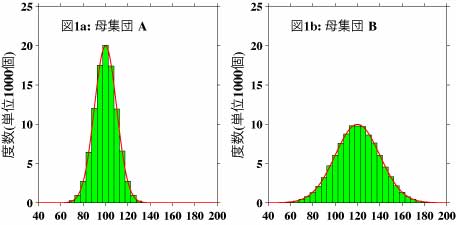
まず、このページで使用するデータですが、図1aは母集団Aの度数分布図を示します。度数分布図とは適当な値の範囲(この図では範囲は5.0としています)のグループでデータを分別し、各グループ内のデータの個数(この図での単位は1000個です)を縦軸に、それぞれのグループの値の範囲の中央の値を横軸にとった図です。この図より、データの値がどのように分布(どういった値のデータが多く、どういった値のデータが少ないか)しているかわかります。図1bは母集団Aとは異なる母集団Bの度数分布図です。これらのデータは、正規分布するような乱数をそれぞれ10万個作成し、それに特定の定数を足しあわせたものです。図にベルのような形をした赤の曲線が描かれていますが、このような分布を正規分布といいます。実際のいろいろなデータは正規分布するようなものが多いのですが、値が大きいほうや小さいほうに裾が伸びたような分布や、頂上が複数あるような場合もありますので、度数分布図を作成し、一応眺めておくのは重要です。また、データの値そのままでは正規分布にはならないが、値の対数を計算する等の若干の操作で正規分布するデータに変換できる場合もあります。母集団から取り出されたサンプルデータの分布については、統計には中心極限定理という便利な定理があり、その定理によれば、通常は母集団の分布の形によらず、サンプルの数が増えるにつれサンプルは正規分布に近づきます。
ここまでで、少し脇道にそれたように感じられる方も多いとは思いますが、データが正規分布していると、統計解析ではいろいろと便利なことがあります。たとえば、平均値は度数分布図で頂上の点であり、個々のデータはそこを中心に左右に同程度に散らばります。従って、平均がそのデータのグループの値を代表するということに異存のある方は少ないでしょう。それ以外にも、正規分布するデータから計算されるいろいろな統計値の性格・意味は過去に詳しく研究されており、あらためてこういった統計値の計算方法について検討したり、その性格・意味を議論する必要がありません。データが正規分布していない場合は、たとえば、平均が、平均であるという以外にデータのどのような特性を示すのかを検討しなければならない場合もあります。以下ではデータは正規分布しているとして話を進めます。
標準偏差及びサンプルの平均値の信頼区間について(計算された平均はどの程度確かなのか)
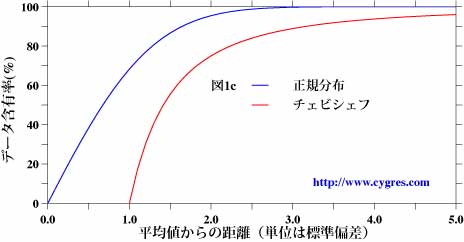
さて、通常は平均に関する統計解析では平均以外に標準偏差も計算します。この標準偏差は平均からの個々のデータの散らばり具合を表します。この母集団Aの平均は100.0で標準偏差は10.0です。また、母集団Bの平均は120.0で標準偏差は20.0です。なお、統計理論ではチェビシェフの定理というものがあり、複雑な計算をしなくてもこの定理により大雑把にどの程度のデータがある範囲内にあるかを見積もることができます。チェビシェフの定理とは、平均値から標準偏差のa倍以内の範囲に全データの1−1/a^2個”以上”(a^2とはaの自乗という意味です。aは1以上でなければなりません。)のデータが含まれるという定理です。正規分布しているデータの場合、どの程度の割合のデータが平均値から特定の範囲内に存在するかを図1cの青線に示します。具体的な値を示しますと、標準偏差の範囲内では68.3%、その2倍の範囲内では95.5%、3倍の範囲内では99.7%となります。図の赤線はチェビシェフの定理の結果ですが、上で”大雑把に”とお断りした理由は、この図で御覧頂けますように、見積もれるデータの個数に”以上”という一言が付け加えられるからです。ただし、チェビシェフの定理は正規分布していない場合でも適用できますので、その点は便利です。
我々は母集団の平均を知るためには、上で記述したように、便宜上しばしば母集団から比較的少数のサンプルを取り出し、そのサンプルの平均を計算し、それを母集団の平均と見なします。しかし、通常このサンプルの平均値は、サンプルのどれか一個を取り替えただけでも変化します。したがって、このサンプルの平均値には不確かさがあることになります。そこで、統計解析ではこの平均値の不確かさを数値で表すために、平均の信頼区間というものを標準偏差を用いて計算します。ただし、この信頼区間の計算時には何%の信頼区間かを指定する必要があります。この%の意味ですが、たとえば95%の信頼区間の例ですと、このようなサンプルを取り出し平均を計算するという操作を数多く繰り返し、それらすべてのサンプルの平均値(通常は毎回異なった値になります)に個々にこの範囲を適用すると、それらのうち95%のケースで母集団の平均が信頼区間の中に収まることになります。これについては、後ほど例を示します。
この信頼区間は標準偏差が大きいほど(すなわち、より散らばっているほど)それに比例して広くなります。これは、例えば、母集団A及びBからそれぞれ5個程度というかなり少数のサンプルデータを取り出し、それらの平均を計算する場合で、それぞれの5個のデータのうち、1個を同じ群の別のデータに取り替えたときに、値の散らばりの大きいデータ群Bのサンプルの平均のほうが、データ群Aのサンプルの平均より大きく変わりやすい、すなわち、データ群Bのサンプルデータの平均の不確かさのほうがデータ群Aのサンプルデータの平均の不確かさより大きいということから類推して頂ければよいかと思います。なお、一般的には信頼区間は99%、95%や90%程度の値で計算することが多いようです。
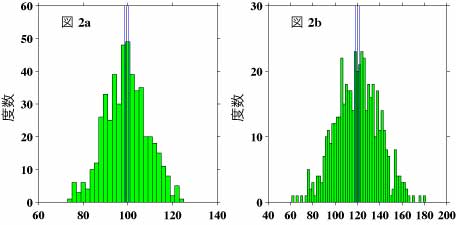
では、ここで、具体的に母集団A及びBから母集団の数の0.5%にあたる500個のデータを取り出してみます。図2a及びbにこれらのサンプルの度数分布図を示します。これらの図中で縦の黒の線がサンプルの平均値の位置を示し、青の線が95%の区間の上限と下限を示します。なお、この図では度数を計算する幅が2.0で、また、aとbで横軸の幅が異なりますのでご注意下さい。
では、ここで95%の信頼区間での95%という数字がどの程度確かなのかを調べるために、上と同じように10万個の母集団から500個のサンプルを取り出して平均を計算するという操作を、母集団のどのデータも1回だけ使用し、計200回繰り返してみます。結果はA群の場合、200回中で母集団の平均値がサンプルの平均の95%信頼区間の中に入らなかった回数は8回で、全体の4%になりました。これは95%の信頼、すなわち5%の誤差にかなり近いのですが、完全には一致しません。このように数限られた試行では95%という値そのものにも、多少の不確かさが生じます。したがって、たとえば95%の信頼区間と96%の信頼区間を計算してその結果を比べるようなことは大抵の場合あまり意味がありません。
○どれくらいの数のサンプルが必要なのか知りたい。
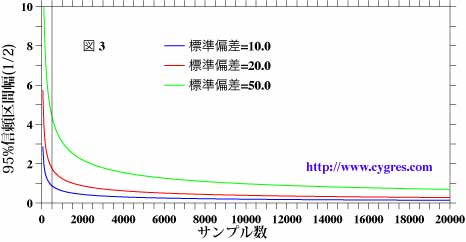
ところで、サンプルの平均の信頼区間の幅はサンプルのデータ数にも影響されます。図3は標準偏差を一定として、信頼区間の幅の半分(平均は平均の信頼区間の中央、すなわち半分の位置にあります)を縦軸に、サンプルの数を横軸にとった図で、標準偏差は青線が10.0の場合、赤線が20.0の場合、緑線が50.0の場合です。黒の縦線は上で採用したサンプル数500の位置を示します。この図のように信頼区間の幅はサンプルデータの数が少ない場合はサンプル数が増えるにつれ急激に狭くなりますが、ある程度迄狭くなると、その後はあまり変わりません。別の言い方をすると、サンプル数を増やすと最初は平均の推定精度が著しく改善されるが、サンプル数がある程度になると、もうそれ以上増やしても平均の推定精度はあまり改善されないということになります。サンプル数を増やすとコストが著しく上昇するような場合はこのような事を考慮して、まず、信頼区間の%の値を決め、次に許容できる誤差を信頼区間の幅の半分として、それよりサンプル数を決めたほうがよいでしょう。上の例の場合、A群ではサンプル数は十分かもしれませんが、B群ではもっと増やしたほうが良いということになるでしょう。
○あるデータの値が平均と”たいして”変わりがないかどうか知りたい。
この疑問がある場合、あるデータの値が上述の信頼区間に入らない場合は、そのデータの値は統計的には平均と異なると見なします。ここで、もし、95%の信頼区間を採用する場合で、もし手元のデータがこの範囲に入らない場合は、5%以下の危険率で平均と異なる、もしくは、平均との差が有意であるという言い方をします。また、もし、手元のデータが信頼区間内に入るならば、母集団の平均も指定した確率でその信頼区間のどこかにあるわけですから、そのデータは平均と”たいして”変わらないと考えてもよいのではないでしょうか。
なお、信頼区間を計算する場合、%の値を指定しなければなりませんが、この%の値次第ではあるデータの値が統計的に平均値と異なったり、その逆になったりします。したがって、信頼区間の%の値はできるだけ客観的に決めるのが一般的です。逆に、信頼区間を%の値を変えて何例か計算し、目的にあう信頼区間の%の値を決める場合もときにはあるようです。この信頼区間は%の値が大きくなるにつれ、広くなり、100%では無限大となります(従って、100%の信頼区間は無意味です)。
○あるグループの平均値と別のグループの平均値との差が”重要”かどうか知りたい。
この疑問がある場合、片方のグループ(甲)の平均の信頼区間を求め、その範囲の中にもう一つのグループ(乙)の平均が入るかどうかを上のようにして判断する方法がありますが、この方法ではグループ甲のデータの散らばり具合は考慮されますが、グループ乙のデータの散らばり具合は無視されてしまいます。これに対し、異なった平均及び標準偏差を持つ2つのデータ群の平均の差については、その統計的性格がわかっていますので、それを利用して判断する方法があります。なお、いずれの方法についても、上と同様に、信頼区間の%を指定する必要があり、その値次第で結論が変わってしまいます。
○あるデータがどのグループに属しているのか知りたい。
この問題は、このページの例では、手元にデータがあり、それがデータ群A又はBのどちらに属する可能性が高いのかを知りたい場合です。基本的な考え方は、手元のデータの値と両グループの平均値迄の”距離”を調べ、より近い側に属すると判断するということなのですが、この”距離”を計算する際には2つの値の単純な差ではなく、それにデータ群A及びBのデータの散らばり具合、すなわち標準偏差の影響を加味する点がみそとなります。上の2母集団の場合、どちらに属するかの境界は約106.67になり、2母集団の平均の中央の110.00よりもA側になります。これは母集団Aのデータの散らばり具合が母集団Bのデータの散らばり具合より小さいので、本来母集団Aに属するデータは母集団Bのデータに比べ、自分の属する母集団の平均により近く分布する可能性が高いためです。なお、このような方法は、複数の特性をもつデータに対しても適用できます。具体的には、たとえば農産物であれば、各試料の重量、長さ、幅、水分含有量、特定の栄養素含有量といったような、異なった特性を総合的に取り入れて計算し、グループ分けの判断の参考にすることもできます。
○母集団の数が少なく、その平均が簡単に計算できる場合の信頼区間の意味は?
たとえば、ある学校のクラスのあるテストの平均の場合を考えてみます。この場合、生徒数はたかだか数十人ですから、その得点の平均や標準偏差を計算し、度数分布図をつくるのはたいした手間ではないでしょう。もし、このテスト結果を母集団と考えれば、これで母集団の平均が計算でき、データの散らばり具合もわかったわけですから推定するべきものはもはや何もないことになります。しかし、もし、手元のテスト結果を、同じレベルのテストを同じレベルの生徒多数に行った場合の1サンプル群と考えたらどうでしょうか?そのように考えられる場合は、平均値の信頼区間を計算することにより、より正確にこのテストの平均が把握できることになります。
また、工場で製造工程の条件を変えて、製品にどのような影響がでるかを調べる場合を考えてみましょう。この場合、試験的に製造する製品の数は普通は限られていて、そのような試作品すべての平均を計算することは容易でしょう。ですが、これは本来もっと多数製造されるべき製品の1サンプル群と考えるべきではないでしょうか?その場合は、上と同様に、平均の信頼区間を計算することにより、より正確に製造工程の条件の変更の影響が見積もれることになります。
○データが比率の場合は?
このページでは平均の値についての話が中心でしたが、値ではなく、賛成と反対、白と黒、正と負のように比率が問題になる場合もあるでしょう。比率の信頼区間等については今までに記述してきた平均の信頼区間等の計算とはやや数式が変わりますが、計算可能で、同じような考え方が適用できます。
○母集団の平均がわからないのにその標準偏差がわかっていることはあまりないのでは?
これは実にもっともな疑問です。このページで取り上げたように、母集団が正規分布している場合は、実はサンプルのデータの標準偏差から母集団の標準偏差及びその信頼区間が計算できます。したがって母集団の平均ではなく、そのデータの散らばり具合を知りたい場合も上で記述した平均値の推定と同様にサンプルから推定できます。なお、サンプルデータの平均の信頼区間は母集団の標準偏差がわかっていない場合でも、計算できます。