コヒーレンスその他諸計算お承ります。お見積もりは無料です。

このページは当事業所で提供するデータ解析業務について、これらの計算の内容の簡単な紹介及びこれらの計算がどのような役に立つのかということを説明するページで、数式や学術用語の使用はできるだけ避けています。このため一部の表現は数学的には厳密ではありません。

このページで紹介している以外の項目については、上の”データ解析”のボタンをクリックして下さい。データ解析のページに記載していないような項目でも計算可能な場合がありますので、データ解析のページに記載していないような項目の計算を希望される場合はメールでお問い合せ頂きますようお願い致します。

コヒーレンスとは(coherency function; 関連度関数）
コヒーレンスは２組の時系列データ間の関連度合を０(＝まったく関連無し)から１(＝完全に関連)迄の値で周波数別に示します。また、両時系列データに関連がある場合、その関連のある変動の両者間の位相関係も示します。この位相とは、たとえば、時系列データAに或る変動があり、時系列データBにも同じような変動があるが、両者間でズレがある場合、そのズレを意味します。この位相について注意して頂きたいのは、時系列データAと時系列データBがまったく同じような変動をしているが、変動に一定の時間差があり、かつ、変動が複数の周波数成分を含む場合は、両者間の位相のズレそのものは、周波数によって異なる点です。これは、周波数の異なる変動は周期も異なり、たとえば、２時間の時間のズレは、周期が４時間の変動では１８０度の位相のズレになりますが、周期が８時間の変動では９０度の位相のズレになることによります。周波数応答関数より求められるゲイン要素は２組の時系列データのうち、片方を入力、片方を出力と考えた場合の、周波数別の振幅関係を示します。

コヒーレンスの計算は２組の時系列データ間のクロススペクトル密度関数とそれぞれの時系列データのパワースペクトル密度関数によって計算されます。コヒーレンスとクロススペクトルの関係は通常のいわゆる相関係数と共分散の関係と同じで、クロススペクトルの大きさをパワースペクトルで規準化したものがコヒーレンスであると考えて良いでしょう。相関係数は、両時系列データ間に周波数によらず一定の時間差で関連があるときは、あらかじめその時間差でデータをずらしてから計算すれば役にたちますが、両時系列データ間に関連はあるが、周波数によって時間のズレが異なる場合はあまり有用ではないと考えられます。コヒーレンスの方が計算はやや複雑になりますが、一旦プログラムを作成してしまえば、最近のパソコンでは数万個のデータで計算しても、ああっという間に計算可能ですので、関心のある時系列データに複数の周波数域で目立つ変動がある場合は通常の相関係数以外にコヒーレンスを計算してみるのも多いに役に立つと考えられます。ただ、他の人に二組の時系列データの関連が大であるということを説明したいが、どの周波数域でどの程度の関連といった複雑な説明は避けたいというような場合は、コヒーレンスを計算し、その結果を参考にして数値フィルタを元のデータに適用し、適当な時間のズレを加えてから相関係数を計算すると便利かもしれません。なお、コヒーレンスは周波数別に関連の高さ（あるいは低さ）は示せますが、関連が高い周波数域で実際エネルギーが大（変動の振幅が大）であるかどうかは、パワースペクトル密度関数の分布を見てチェックする必要はあると思われます。周波数のかなり広い部分で関連が高いが、その部分でのエネルギーは小なため、相関係数は小さくなるという場合もあるかもしれません。なお、周波数応答関数は２組の時系列データ間のクロススペクトル密度関数および、入力にあたる側の時系列データのパワースペクトル密度関数によって計算されます。これらの信頼区間はスペクトル密度関数の信頼区間に準じて定義されます。

なお、当事業所での料金は基本的には時間制を採用させて頂いておりますので、作図を含めなければ、コヒーレンスと通常の相関係数の計算料金の差はほとんどありません。

コヒーレンスの実用例
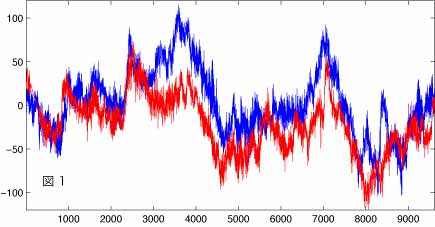
図１は太平洋赤道上東経１５６度（青）及び１６５度（赤）で観測された流速の東西成分の変動の時系列プロットです。あまり一般の方が関心を持たれるようなデータではないと思いますが、時系列データということでは特別に変わったデータでもないということで、ご容赦ください。
当事業所では海洋・水産・気象関連のデータ処理・解析や数値計算を主に行っていますが、他分野の諸計算業務についてもお受け致します。個人やNPO、NGOのお客様も歓迎致します。

当事業所について

お問合せは
->こちらへ<-
ここではそれぞれの時系列で９６２０個のデータがありますが、図を見やすくするために赤線を縦方向に少しずらしてあります。この図を一見すると、１５６度と１６５度の流速は非常に関連が高いという印象を受けます。ただし、こういった図の場合、私たちはどうしても目立つ変動に注目してしまい、この例では一ヶ月（横軸目盛りで24x30=720）から数ヶ月のの変動に目を奪われがちです。

そこで、図２aにこの両データ間のコヒーレンスを示します。コヒーレンスは長周期の部分では0.8以上ですが、周期が減少するにつれ急激に減少し、周期約４０日（縦の黒破線）で約0.5になり、周期約２０日で最低となります。それ以下の周期では値は大きく変動しますが、低いままです。この図より、両データで関連が高いのは長周期の変動のみということがわかります。

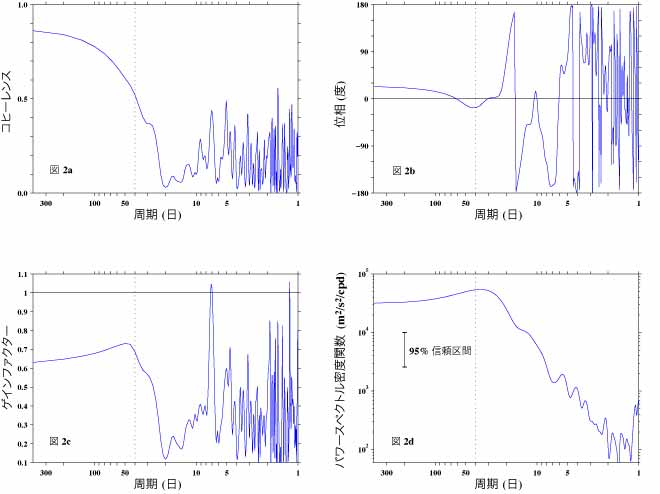
次に図２bに位相を示します。この図で黒の実線は位相がゼロであることを示します。図２aでコヒーレンスが高かった部分では位相は周期の長いところでは正で、周期が減少すると負になっていますが、これらの値は統計的には位相差があるとは言えません。言い換えれば、統計的には両者間に位相差は無いといっても良いということです。なお、正値は165度での変動が156度での変動に先行することを意味します。

図２c は周波数応答関数より得られるゲイン要素を示します。これは変動の両者間の振幅比を示します。この図より165度の変動は156度での変動よりほぼ全周波数域で小（値が1.0より小）であることがわかります。なお、両者間のコヒーレンスの高い部分では、165度の変動は周期が減少するにつれ相対的にやや大きくなる傾向があるようです。

図２dは156度のデータのパワースペクトル密度関数を示します。この図によれば周期４０日以下の変動も決して著しく小さいわけではないことがわかります。したがってコヒレーンスが小さい部分の変動も決して無視できない可能性を示します。

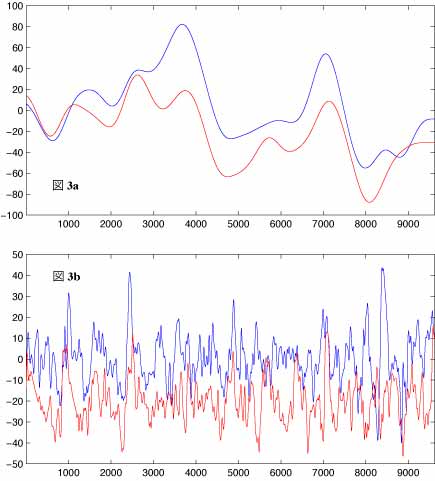
図3aは周期４０日以下の変動をカットするローパスフィルタを適用した後のデータの時系列プロットです。この図により、周期４０日以上の変動は両データで非常によく似ていることがわかります。なお、相関係数は時間差を与えてやると最大で0.84となります。
この図では165度（赤線）の比較的短周期の変動はやや振幅が相対的に大きいようですが、これは図2cで示される結果と一致するようです。図3bは周期４０日から２日迄の変動を通過させるバンドパスフィルタを適用した後のデータの時系列プロットです。最初の３０００個あたりまでの部分を除くと、両データはまったく関連が無いように見えます。相関係数は時間差を与えても最大で0.26です。また、最初の３０００個あたりにしても、関連があるように見えるのは比較的長周期の変動のみで、図2aより、このフィルタの通過帯域上限の４０日あたりのコヒーレンスは約0.5ですので、この図に見られる長周期の変動に相互関連が見られてもおかしくありません。ここで重要なのは、図2dで得られた印象と同じく、図3bで示された変動の振幅は図3aで示された変動に比べ決して振幅が小ではなく、図１を見た際に得た両データの関連は高いという初印象はあまり正確ではなく、”長周期部分で”という条件を付けねばならなかったという点でしょうか。このようにコヒーレンスは２つの時系列データの関連具合を調べる際には大変便利です。
なお、赤道上東経156度と165度の間の距離は約1000kmもあります。長周期部分では確かにこの両データの関連はかなり高いのですが、これは赤道という地球物理的に非常に特徴的な場所であるためです。この事について関心のある方はこちらへ。

３組以上の時系列データの相互関連を調べたい
では、３組以上の時系列データの関連を調べたい場合はどうでしょうか？例えば、ここに１０組の時系列データがあるとします。いま、一組の出力に対し、９組の入力データがあるというような場合はコヒーレンスは９通りあるので、９枚の図を作成し、それを並べて眺めるなり、あるいは図を工夫して１枚の図にして調べるといったこともそれ程たいしたことではないでしょう。しかし、もし、１０組のデータのどれが出力ということでもなく、それらすべてに共通する変動を調べたい場合はどうでしょう？１０組のデータから２組の時系列データを取り出す組合せは４５通りもあります。４５枚ものコヒーレンスの図を机の上に並べて、それを眺めて共通する変動を調べるというのはちょっと大変です。このような場合はEOF解析をおすすめします。なお、EOF解析とは時系列データに適用する主成分解析のことですが、このことばは気象・海洋関連分野の”方言”のようです。

近日中にお取り扱いするデータの形式、計算内容、計算結果の内容及び形式やデータ授受方法といった業務全般を定型化することでコスト削減及び納期短縮を図った低価格の計算サービスを開始致します。詳細は->ここ<-をクリックください。