










お取り扱いするデータの形式、計算内容、計算結果の内容及び形式やデータ授受方法といった業務全般を定型化することでコスト削減及び納期短縮を図った低価格のスペクトル密度計算サービスを開始致しました。詳細は->ここ<-をクリックください。
このページは当事業所で提供するデータ解析業務について、これらの計算の内容の簡単な紹介及びこれらの計算がどのような役に立つのかということを説明するページで、数式や学術用語の使用はできるだけ避けています。このため一部の表現は数学的には厳密ではありません。
このページで紹介している以外の項目については、上の”データ解析”のボタンをクリックして下さい。データ解析のページに記載していないような項目でも計算可能な場合がありますので、データ解析のページに記載していないような項目の計算を希望される場合はメールでお問い合せ頂きますようお願い致します。
4 複素EOF(時間領域)
4-1 複素EOF(時間領域)とは?
複素EOF(時間領域)は解析したい複数組の時系列データ上に存在する変動が各データ組間で関連してはいるがデータ組間で位相差がある場合(時間差ではありません)に使用されます。手法としては、元のデータに複素平面上で90度位相を変えた成分を付加し、後は前述のEOFと同じような方法で計算しますが、計算方法や数学的な詳細についてはこのページの趣旨に添いませんので省略致します。
4-2 例
ここでは、複素数を用いないEOFの例と同じデータ(図1)を使用しますので、入力データの詳細についての説明は省略致します。図6aは40mの深さでのモード1(青線)及びモード2(赤線)の成分の時系列です。なお、モード2は振幅が小なのでこの図では3倍にして表示しています。
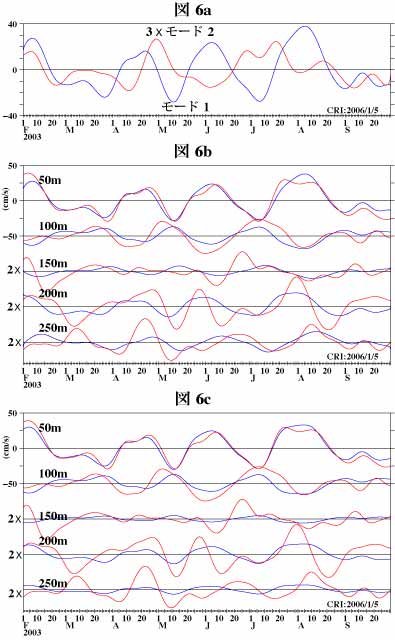
複素EOF(時間領域)では深さによる振幅の変動のみではなく、位相の変動も許容できますので複素EOF(時間領域)の結果生成される時系列は深さにより変動の大きさのみではなく、形も変化します。ここで、ご注意頂きたいのは、位相の差が一定ということは、時間の差が一定ということではないということです。例えば今2組の時系列データ間に90度の位相差があるとします。この場合周期4時間の変動は両者間で1時間(90/360X4=1です)の差があり、周期40時間の変動は両者間で10時間の差があることになり、片方の時系列を適当にずらしてもう片方の時系列に重ね合わせようとしてもうまく重なり合いません。
さて、図6bに図1で示した深さでのモード1の成分(青線)と元のデータ(赤線:図1の青線と同じです)を示します。なお、150~250mの図は値が小さいので2倍にして表示しています。図6cは前の複素数を用いないEOFの結果で、比較のためにここに表示しました。浅いところではどっちもどっちといった感じですが、250mあたりですと複素EOF(時間領域)のほうがよく一致しているのが御覧頂けるのではないかと思います。
図6dは図2bと同様に固有値を示し、各モード(全部で23成分あります)が元の全23組の時系列データに含まれる変動をどの程度の割合で含むかを示しています。モード1はここでは60.2%となり、前のEOFの結果に対し6.7%高くなっています。
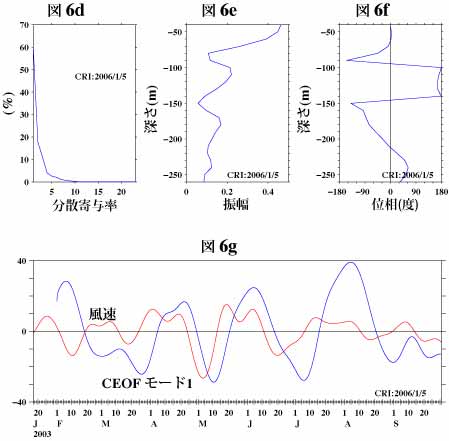
図6eと6fはモード1の振幅と位相を示します。この振幅と位相は固有ベクトルより得られる情報で、位相については40mの値をゼロとしてそれからの相対的な差です。ここで、位相-180度と+180度は実は同じで、90~100mで位相が大きく変化しているように見える部分は値が-180度を超えそれが正の値として表示されているのであって、位相が大きく変化しているわけではありません。140-150mで位相が大きく変わっている部分も同様です。位相が+または-180度いうのは変動が反転している場合ですが、この図より100~140m付近の変動はその上下の深さでの変動と逆の変動をしていることがわかります。
これ以上の解析は本ページの趣旨に添いませんので省略しますが、図6eと6fより深さに伴いモード1の変動の大きさがどのように変化し、そのずれがどのようになっていくのかがわかります。このような情報は現象を解析するにあたって重要なヒントになる可能性があります。図6gは図3aと同様に、この複素EOF(時間領域)で計算したモード1の40mでの時系列変化と風の時系列変化を比較するための図です。
4-3 複素EOF(時間領域)を使用する際の注意
前に複素数を用いないEOFを使用する際の注意について記述致しましたが、それらに加え以下のような注意が必要です。
(1) 位相差について
位相差と時間差については上で記述致しましたが、もし入力データの各組間の変動に一定の時間差がある場合は、入力データをその時間差によって適当にずらして複素数を用いないEOFで計算したほうが良いと思われます。なお、このような入力データに比較的通過帯域幅の狭いバンドパスフィルタを適用すると、その狭い通過帯域のなかでは位相差も比較的一定になるのでそれを用いるという方法もありますが、バンドパスフィルタの通過帯域をあまり狭くすると弊害もあるので注意が必要です。他の方法としては後述の周波数領域EOFを用いることも考えられます。
5 ベクトル形式のデータのEOF(複素、時間領域)
5-1 ベクトルデータのEOFとは?
解析したいデータは値の大小のみではなく方向の情報を持つようなベクトル形式の場合もあるでしょう。上の例では海洋中の流速を取り上げましたが、流速は本来ベクトルで、上では値の大きさと方向を組み合わせて東西方向の成分のみを取り出したものを使用していますが、これとは別に南北方向の成分も同時に存在します。赤道直下というのは海洋物理的にやや特殊な場所になるのでここでの例では流速の解析を東西成分のみで行ったのですが、実際には両方の情報を組み合わせて同時に解析を行いたい場合もあるでしょう。このような場合は上で示した例ですと、流速の東西方向の成分を実部、南北方向の成分を虚部とした複素数で入力データを作成し、後は通常の時間領域のEOFと同様の方法で計算します。
6 周波数領域EOF(複素数)
6-1 周波数領域EOF(複素数)とは?
周波数領域EOFとは前の時間領域の各EOFと異なり、入力時系列データ各組間のクロススペクトル密度関数の行列を作り、その固有ベクトル及び固有値を求める計算です。ここで、クロススペクトル密度関数は、非常に大雑把にいうと、前の時間領域の各EOFでの共分散に相当しますが、2つの時系列データ間の関係を周波数別(または周期別)に示し、これにより相関係数に類似したコヒーレンス(関連度関数)が計算できたりします。コヒーレンスは通常の時間領域の解析では相関係数に相当するものですが、値は0(無関連)から1(関連)の範囲となり、相関係数での正負の符号に相当する情報は位相として示されます。このクロススペクトル密度関数の行列は通常はデータの期間の長さで決定される一定の周波数間隔毎に作成できますので、周波数領域EOFはそれぞれ個別の周波数(帯域)で他の周波数(帯域)とは独立して計算することになります。このため、周波数領域EOFを用いる場合は入力時系列データ各組間の変動の位相差は周波数(帯域)によって異なってもかまいません。また、特定の周波数領域のみを取り出すようなフィルタ操作は不要になります。
6-2 例
ここではまた前と同じデータを使用しますが、このタイプのEOFは計算したい周期の幅が限られていてもバンドパスフィルタを適用する必要がないので、バンドパスフィルタは使用していません。図7aは周期20日から150日の区間(上の時間領域のEOF計算時に適用したバンドパスフィルタの通過帯域幅に合わせています)の各周期帯でのモード1の強さを等高線図の形式で示しています。
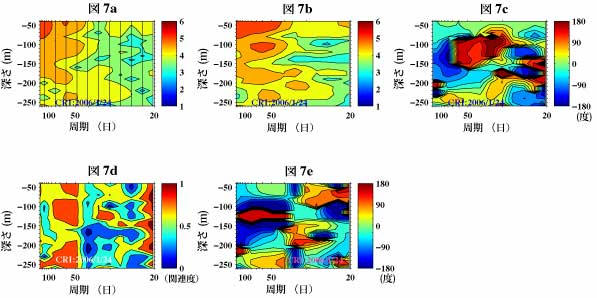
この図は縦軸が深さで横軸が周期ですが、この図を作成するために周期242日から20.17日迄の12のバンドで個別に12回EOFの計算をしています。これらの周期帯の中心周期は図中の縦の黒線で示していますが、前述したように通常はデータの期間長によって決まる一定の周波数(周期の逆数に比例します)間隔になります。なお、ここでのモード1の強さとは比較のためにモード1の振幅をパワースペクトル密度関数(図7b)と同じ単位にしたものです。ここで、パワースペクトル密度関数は時系列データに含まれる変動の強さを周波数(周期)別に示します。なお、クロススペクトルを計算する際には周波数領域で平滑化(以下FDSと略)するという操作を行いますが、ここでは周波数による違いを細かく見るために3バンドという狭い幅のものを使用しています。この周波数領域での平滑化とは元のデータより計算した”生”のクロススペクトルの各周波数成分を移動平均のように隣接する周波数成分の値を用いて平均化する操作で、その際に重みを付ける場合も付けない場合もあります。なお、この図では値の対数をとって表示していますので、図で値が1異なると実際の値は10倍異なり、この図での濃青(2.0)と濃茶色(6.0)では値が10000倍異なります。
さて、図7bより元のデータ上の変動は周期40-80日辺りで浅いところ、110m周辺、180m周辺及び230m周辺で大きくなっていることがわかります。浅いところではさらに長い周期迄変動が大きくなっています。さらに細かく見ると110m付近での50日付近の変動は同じ深さの80日より長い周期や45日程度より短い周期の変動に比べ100倍またはそれ以上大きくなっています。図7aと図7bを比較すると周波数EOFのモード1の強さの分布(図7a)は元のデータ上の変動の強さの分布(図7b)によく似ていますが、値そのものはやや小さくなっていることがわかりますが、この小さくなった分は他のモードに含まれていることになります。
図7cはモード1の位相を示しますが、以前と同様に+180度と-180度は同じですので、周期30-70日辺りの70-100m付近で濃紺から濃赤に変わっている部分や140-160m付近で濃赤から濃紺に変わっている部分では位相が大きく変わっているわけではありません。この図によれば、等値線は主に水平方向に伸びていて、これにより位相の変化は深さ(縦)方向は大きく周期(横)方向には小さいことがわかります。従ってこの例のようなケースでは4-1で使用したような複素EOF(時間領域)での位相差が周期に無関係に固定されるという問題はあまり深刻ではないと推測できます。
図7dはこの流速の周波数EOFのモード1と、時間領域のEOFの例で使用した風の東西方向の成分との関連を示す図で、コヒーレンス(関連度関数)です。図7dより、周波数EOFのモード1の周期40-80日付近や30日付近の変動は風と強く関連していることがわかり、図7eより周期40-80日付近の変動については100-150m付近とその上下では位相が180度近く異なる、すなわち変動が反転していることがわかります。
これ以上の解析はこのページの趣旨に添わないので省略しますが、このように周波数領域EOFは時間領域EOFに比べると周波数(周期)による変化がわかるようになるのが特徴ですが、計算量はかなり増加します。また、後述するようにEOFの結果から新しい時系列を生成するような用途には向いていません。
6-3 複素EOF(時間領域)と周波数領域EOFの関係
複素EOF(時間領域)を計算する際に事前に非常に帯域の狭いバンドパスフィルタを適用すると、周波数領域EOFを用いて該当周波数域で計算した結果と同じような結果が得られます。しかし、通過帯域内での特性は平坦で歪みが少なく通過帯域外は減衰が大きいといった理想的な狭通過帯域巾のバンドパスフィルタを実現するのは困難です。もしEOFによって新しい時系列データを作成する必要がなく、入力時系列データ間に共通する変動の位相や振幅が周波数によってどのように違うのかを調べたいのであれば、周波数領域EOFに代えてフィルタと複素EOF(時間領域)を組み合わせて使う実用的なメリットはあまりないと思われます。
ここでは、例として両者を比較するために複素EOF(時間領域)計算前に適用するバンドパスフィルタの通過帯域幅を狭めるのではなく、逆に周波数領域EOF計算時に適用するFDSの幅を広くして再計算してみました。図8aの青線は周波数領域EOFのモード1の位相で赤線は複素EOF(時間領域)のモード1の位相です。ここで表示している周波数領域EOF計算時にはFDSによって121~20.2日といった広範囲の周期を含むバンドを使用しており、複素EOF(時間領域)については通過帯域幅を同じにしたバンドパスフィルタを計算前に適用しています。また、いずれの計算時にもデータは40~80mのもののみを使用しています。図8bはこれらのEOFの強さで、周波数領域EOFについてはFDSのバンド幅(12)倍しています。なお、強さの単位は元のデータ上の変動の強さ(黒線;分散)のものに合わせています。
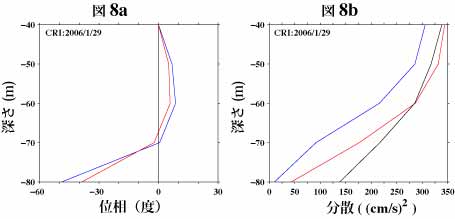
ここでの比較はかなり広い周波数幅の計算結果を用いて行ったわけですが、それでも、少なくともこのデータの場合については、両方法間での差はあまり無いことがお分かり頂けるのではないかと思います。
6-4 周波数領域EOFを使用する際の注意
(1) 他の時系列データとの比較
周波数領域EOFの結果得られる各モードと他の時系列データを比較するには、上の例のように周波数領域EOFの結果と比較対象の時系列データとの間のコヒーレンスを調べれば良いでしょう。ただ、コヒーレンスだけでは何となく不安だと感じられる場合は、図7a及びbのような図を作成し、時系列データに興味がある部分の周波数域のみを通すバンドパスフィルタを適用して比較して見てみると良いのではないでしょうか。
このような方法を取ることをお勧めする理由は、周波数領域EOFは時間領域のEOFのように新しい時系列データを生成して、他の要素の時系列データと比較するような用途にはあまり向いていないという点にあります。周波数領域のEOFでは個別の周波数で計算しなければならないため、入力データの組数が多く関心のある周波数域が広い場合は計算時間が多く必要になりますが、単一の周波数帯でのみ周波数領域EOFを計算しその結果を用いて時系列データを生成すると、ただ単なるまったく一様な正弦波にしかなりませんし、少々周波数帯を増やしても結果として生成できる時系列は非常に単調なものとなり、比較できるような特徴があまりでてきません。したがって、時系列データを生成する目的で周波数領域EOFを計算する場合は相当数の周波数帯で計算し、それらを足し合わせなければなりませんが、周波数帯を増やしすぎるとこんどは注目しているような変動が存在しない周波数帯まで含めることにもなりかねません。また、FDSによって時系列が”歪め”られてしまいます。
目的が新しい時系列データの作成であるならば、時間領域のEOFを使用したほうが”素直”ではないかと考えられます。
(2) 同じモードでも周波数が異なれば全然異なった性質のものかもしれません
周波数領域EOFの計算は各周波数(周期)帯で個別に行われます。図7aの例では縦の黒線がそれらの周波数(周期)帯の中心を示します。実際の計算時には上で記述したようにFDSを適用するので、ある特定の周波数(周期)帯での計算結果は隣接する周波数(周期)帯の変動にも影響されますが、はるかに離れた周波数(周期)帯の変動は全く影響しません。図7の例ではFDSの幅は3バンドなので、ある特定の周波数(周期)帯での結果はその周波数(周期)帯及び左右隣接する周波数(周期)帯での変動のみに影響されます。このような場合、例え同じモード1でも周波数(周期)の差がこの影響域を超えている場合は計算上は全く無関係のものとして行われているので、両者の性質が同じであるかどうかはさらなる解析を行わない限りまったくわかりません。場合によれば、同じ外部要因によって生じた変動でもある周波数域ではモード1になり、別の周波数域ではモード2になるようなことがあるかも知れません。したがって図7のような図は例としてはともかく、実用に供する場合は解釈に注意する必要があります。
実際、図7dでは周期約40日を中心とした狭い範囲でコヒーレンスが周辺よりかなり低くなっていますが、モード2ではこの部分では逆に周辺より高くなっています。 図9aは風の東西成分とEOFを適用していない流速の東西成分(元データです)とのコヒーレンスを計算しその深さ-周期分布を表示したものです。図9bは図7dと同じ図で、風の東西成分と流速の東西成分の周波数領域EOFのモード1との間のコヒーレンスを示します。図9cは風の東西成分と流速の東西成分の周波数領域EOFのモード2との間のコヒーレンスです。
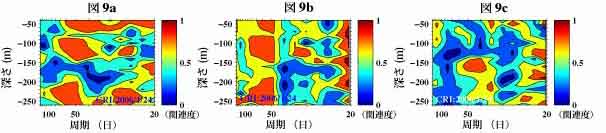
図9aよれば表示している周期帯の中では風と流れの間のコヒーレンスが高い部分はかなり広いのですが、周期約40日を中心とした1バンドではコヒーレンスの高い部分は図9cよりモード2になっているようです。図7a及び7bより、この周期域付近でのモード1は150m程度より浅い部分での変動を強くあらわしているようですが、詳細はさらなる解析が必要です。この周期域や周期30日以下で200mより深い部分を除くと、風の東西成分と流速の東西成分の周波数領域EOFのモード1とのコヒーレンス(図9b)の高い部分はモードに分解せずに計算したコヒーレンス(図9a)の高い部分より広くなっています。
7 ロータリー(回転;Rotary) EOF(複素、時間領域)
7-1 ロータリーEOFとは?
海洋では、変動が時計廻りまたは反時計廻りに回転する現象がありますが、ロータリーEOFはそのような現象を解析するために用いられています。具体的には流速の東西方向の成分を実部、南北方向の成分を虚部とした複素数で入力データを作成し、後は通常の周波数EOFと同様の方法で計算します。海洋のデータ解析に詳しい方はロータリースペクトルの考え方と類似していることに気が付かれたと思います。現在当事業所では、この方法の適用が適切なデータがありませんので、例は省略致します。
このページはEOFに関する御説明のページの2ページ目になります。1ページ目を御覧になりたい方は下左の矢印をクリック下さい。
お問合せは
->こちらへ<-
