お問合せは
->こちらへ<-

パワースペクトル密度計算 (スペクトル解析)
小額定型計算 PD001A/B
小額定型計算業務はお取り扱いするデータの形式、計算内容、計算結果の内容及び形式やデータ授受方法といった業務全般を定型化することでコスト削減及び納期短縮を図った計算サービスです。科学、技術研究のみではなく、商業や工業のいろいろな分野のデータの解析にご利用下さい。小額定型計算業務については->こちら<-をクリック下さい。
図を含む本文書の著作権はCygnus Research Internationalに帰属します。無断転載はお断り致します。
PD001A/B ユーザーガイド 6/7
目次
(1章) PD001シリーズの要約
(1-1) PD001シリーズで行う計算について
(1-2) お客様がご指定できる計算設定項目の要約
(1-2-1) トレンド除去; 全てのケースで個別に指定
(1-2-2) PSDの値の信頼区間のパーセンテージ; 全ケースで同一の値を指定
(1-2-3) テューキー窓関数のテーパー比; ケースB1、B2及びB3のみ適用 値は個別に指定
(1-2-4) 周波数領域での平滑化(以下FDSと略)ビン巾; ケースA1、B1及びC1の3ケースを除く全ケースで個別に指定
(1-3) 計算手法
(1-4) 入力データ(お客様のデータ)について
(1-5) プロダクツ
(1-5-1) 結果ファイル
(1-5-2) PDF形式の図
(1-6) 料金、納期およびご発注手順
(1-7) 個人情報、お客様のデータに関する情報保護
(2章) プロダクツの詳細及びその使用例
(2-1) 結果ファイル
(2-1-1) 結果ファイルのフォーマット(形式)
(2-1-2) 結果ファイルに記述する計算結果の内容
(2-1-2-1) 周波数 (Frequency)
(2-1-2-2) 周期 (Period)
(2-1-2-3) PSD (PSD)
(2-1-2-4) PSDの信頼区間 (Conf Int)
(2-1-2-5) 分散のパーセンテージ (% of Var)
(2-1-2-6) 振幅 (Amplitude)
(2-1-2-7) 位相 (Phase)
(2-1-3) 結果ファイルに書き出された情報の利用方法及び使用例
(2-1-3-1) 結果ファイルの値を用いて独自の図を作成したい場合
(2-1-3-2) PSD及びPSDの信頼区間の使用方法
(2-1-3-3) 特定の周波数での変動の巾(大きさ)を知りたい場合
(ケース1) 信号は振幅が一定の単一の周波数の三角関数で表される場合
(ケース2) 信号は振幅が一定の異なった周波数の三角関数を足し合わせたもので表される場合
(ケース3) 信号は単一の周波数の三角関数だが、振幅が時間とともに変動する場合
(ケース3-1) 信号の振幅の変動そのものが三角関数の形の場合
(例1) 信号は三角関数で周波数はf0。信号の振幅は周波数f1の三角関数の形で変動
(例2) 信号は三角関数で周波数はf0。信号の振幅は定数に周波数f1の三角関数を足し合わせた形で変動
(ケース3-2) 信号の振幅の変動そのものは三角関数ではない場合
(ケース4) 信号は周期的だが、三角関数の形ではない場合
(2-1-3-4) 特定の周波数域内の変動が全体の変動と比べてどの程度強いのかを知りたい場合
(2-1-3-5) 簡易デジタルフィルター(PD001Aのみ適用)
(2-1-3-6)データ中の値の変動の振幅を求める他の方法
(2-2)図
(3章) PD001シリーズ用のデータファイルの作成手順例
(4章) 各種指定項目の設定について
(4-1) トレンド除去;有無 無指定時は有
(4-1-1) トレンドとは? 除去の目的は?
(4-1-2) トレンド除去の例
(4-1-3) トレンド除去で問題が発生する例
(4-2) テューキー窓関数のテーパー比;%で表したテーパー比 無指定時は10%
(4-2-1) 窓関数を適用する理由
(4-2-2) 窓関数の適用とは
(4-2-3) ハニング窓関数;使用すると問題が生じる場合について
(4-2-4) 本小額定型計算業務 PD001Aでハニング窓関数を適用したPSDのみではなく、窓関数非適用及びテューキー窓関数を適用したPSDも計算する理由
(4-2-5) ハニング窓関数によるデータ両端近くの減衰を少なくする方法
(4-2-6) 窓関数が持つFDSに似た効果について
(4-2-7) IFDSは必ずしもPSDを平滑化しない
(4-2-8) 窓関数適用によるPSDや振幅スペクトル減衰に対する補正
(4-2-9) 窓関数適用時の補正の効果
(4-2-10) テューキー窓関数のテーパー比がPSDに与える影響
(4-3) 周波数領域での平滑化(FDS)ビン巾; 1、3、5、7等奇数 無指定時は無し(1)、3及び7
(4-3-1) PSDに対するFDS
(4-3-2) 振幅スペクトルに対するFDS
(4-3-3) FDSを適用した場合の周波数解像度
(4-3-4) FDSに代わる他の平滑化法
補足1 コンピュータを用いて計算をする際に生じる誤差について
補足2 パワースペクトル密度関数のスペクトル漏れと窓関数の関係について
補足3 データ長が短いと単一のピークが現れ、長いとツインピークが現れる理由
補足4 S1のトレンド除去により付加される直線成分のPSDの悪影響に対するS1とSRの周波数の関係
(4-3)周波数領域での平滑化(FDS)ビン巾; 1、3、5、7等奇数 無指定時は無し(1)、3及び7
本小額定型計算業務PD001Aで行うFDS(周波数領域での平滑化)はPSDを一旦計算した後に計算されたPSDに対して適用する単純な重み無しの移動平均です。たとえば平滑化ビン巾を5にした場合は以下のようになります。

ここで上式の右辺の項はどれも公平に取り扱われていますので、重み無しということになります。なお、移動平均は時系列データを滑らかにする目的に色々な分野で広く使われています。
(4-3-1)PSDに対するFDS
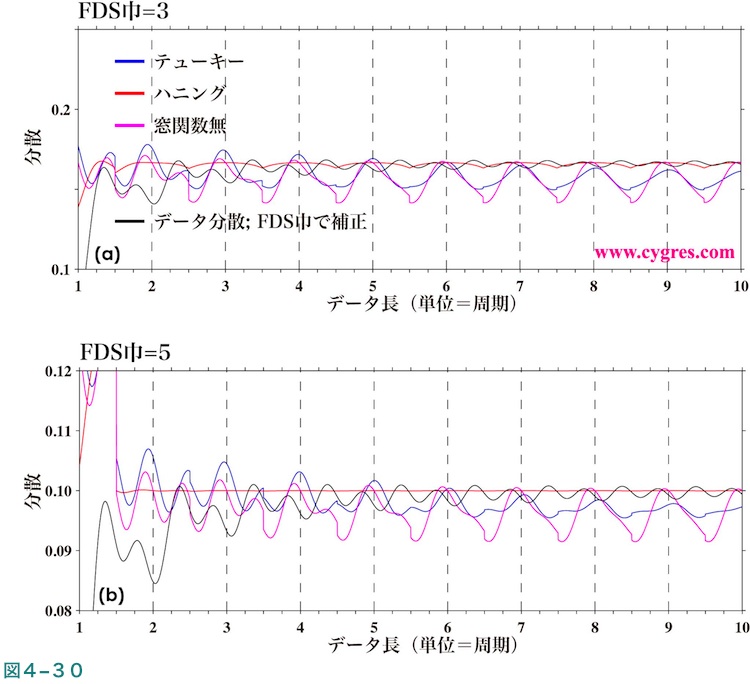
図4-30(a)は平滑化巾3ビンのFDSを適用した信号ビンのPSDにビンの周波数巾を掛けた値、すなわち平滑化を行った信号ビンの分散がデータが増えるにつれどのように変化するかを示します。ここで使用したデータは単一の周波数の三角関数のみを含むもので図2-4で使用したデータと同じです。なお、この図中のデータの分散(黒線)は比較のために3で割っています。この図と図4-24(b)を比較すると、FDSを適用したことにより信号ビンの分散とデータの分散の差がかなり小さくなったことがわかります。図4-30(b)は平滑化巾を拡げて5ビンにした結果ですが、信号ビンの分散とデータの分散(5で割っています)の差がさらに小さくなっています。これらの図によりPSDに対するFDSは有効であることがわかります。なお、図4-30(a)でデータの分散を3で割ったようにFDSを適用するとPSDの値が小さくなりますが、これはFDSを適用すると(4-3-3)で記述するようにビンの周波数巾を実質変えたことになるからです。
(4-3-2)振幅スペクトルに対するFDS
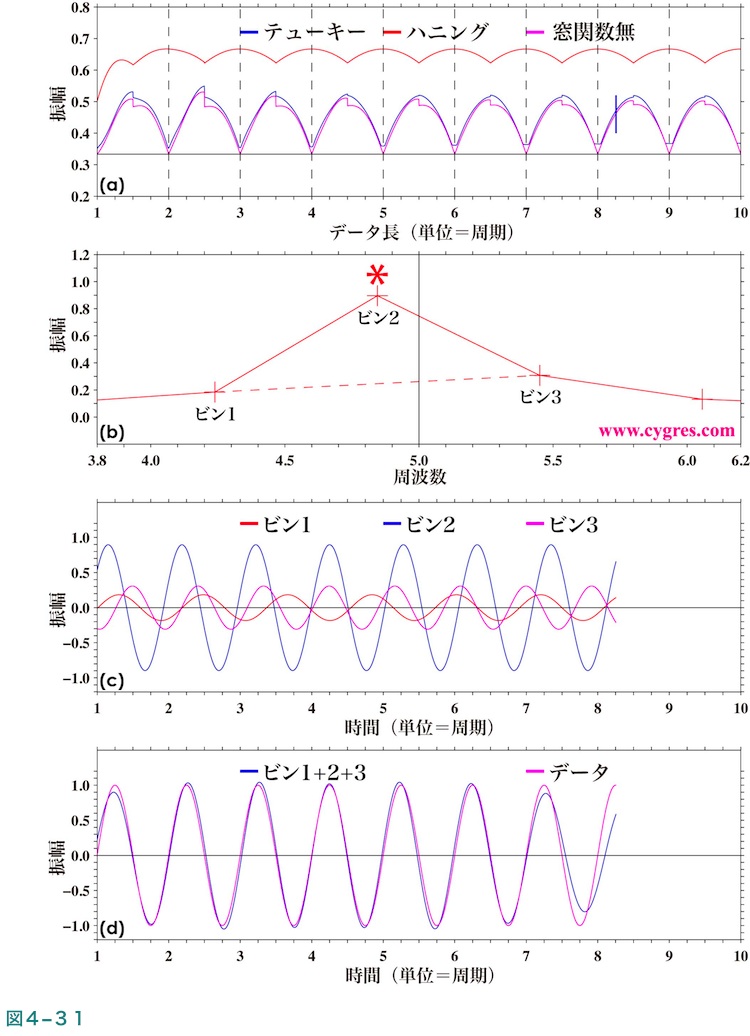
(2-1-3-3)(図2-10、図2-17)で記述したように振幅スペクトルに対してはFDSの適用は不適切です。ここでは最初に窓関数非適用の場合についてなぜFDSがうまく機能しないかについて説明します。図4-31(a)は平滑化巾3ビンのFDSを適用した信号ビンの振幅がデータが増えるにつれどのように変化するかを示した図です。ここで使用したデータは単一の周波数の三角関数のみを含むもので、この図は図2-10(a)と基本的には同じ図です。この図中の水平の黒の実線は実際の信号の振幅を3で割った値で、PSDの場合と同様にこの値がFDSを適用した信号ビンの実際の振幅になります。なお、図中の縦の黒の破線は周波数一致が成立しているデータ長を示します。この図より周波数一致が成立していないデータ長ではFDSを適用した信号ビンの振幅は実際の信号の振幅より大きくなります。ここで、図4-31(a)で図の横軸位置8.0よりやや右にある縦の短い黒の実線で示した図2-4においてはデータ長Bにあたるデータ長の場合を調べてみます。図4-31(b)はこのデータ長の場合の信号ビン周辺の振幅スペクトルの詳細を示します。この図中で中央にある縦の黒の実線は信号の実際の周波数、プラス記号(+)は各ビンの周波数及び値を示します。なお、米記号(*)は信号ビンを示します。ビン1、2(信号ビン)及び3の振幅はそれぞれ約0.18、0.90及び0.31ですので、ビン2における平滑化巾3ビンのFDSを適用した振幅は(0.18+0.90+0.31)/3=0.46となり、実際の信号の振幅1/3=0.33...より大きな値になります。図4-31(c)はこれらのビンによる時系列変動を式(3)により個別に再現したものを示します。この図よりこれらのビンによる時系列変動は”山”や”谷”といった部分が同じ水平位置(時間)にはないことがわかりますが、これらのビンは周波数も位相も互いに異なりますので、このように各ビンによる変動が揃っていないのはむしろ当然と言えます。図4-31(d)の青線はこれらの3つのビンによる時系列変動を足し合わせた結果ですが、この青線はデータ(赤線)とほぼ一致し、変動の振幅は概ね1.0となっていて、各ビンの振幅を単純に足し合わせた0.18+0.90+0.31=1.38に比べかなり小さな値になります。この差は単純に振幅の値のみで計算すると各ビンの周波数や位相の違いを一切無視してしまうために生じています。FDSについても同様の事が言えます。なお、図4-31(d)の青線は式(3)により信号ビンを中心とした両隣のビン、計3ビンの周波数域を総合した変動になり、これだけでデータ全体の分散の93%に相当します。データとの差は主に図の両端部に現れています。
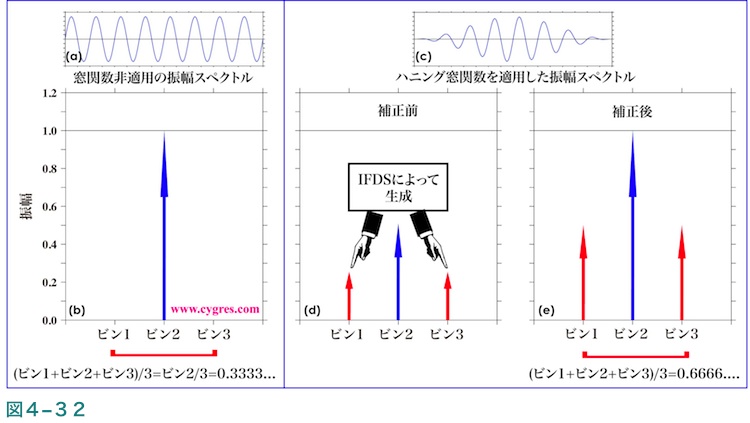
図4-31(a)において縦の黒の破線で示したデータ長は周波数一致が成立している場合のデータ長ですが、周波数一致が成立している場合は図4-32(b)に示すように信号ビン(ビン2)以外のビンの振幅は実質0になります。この場合は図4-31(b)中でのビン1及びビン3の値が0で、ビン2の値がほぼ1.0になるという事ですので、FDSを適用するとほぼ実際の信号の振幅1/3と一致します。
次にハニング窓関数を適用した場合についてですが、その場合は図4-31(a)で示されるように周波数一致が成立していても振幅が実際の信号の振幅に比べかなり大きくなります。図4-32(c)は周波数一致が成立している長さのデータ長のデータ(図4-32(a))にハニング窓関数を適用した結果を示します。ハニング窓関数を適用すると周波数一致が成立している場合でも(4-2-6)で記述したように信号のピークの巾が広がり図4-32(d)に示すようにビン1及びビン3の振幅もゼロではなく信号ビンであるビン2の半分の値となります。ここで、上で記述した補正を行って図4-32(e)に示すようにビン2の値を実際の信号の振幅と同じ(FDS適用前ですのでこの例では1.0です)値にすると、ビン1及びビン3の値は0.5になり、それに対し平滑化巾3ビンのFDSを適用すると2/3になります。これに前述した窓関数非適用のケースと同じ問題が加わりますので、ハニング窓関数を適用した場合の振幅スペクトルにFDSを適用すると、実際の信号の振幅よりかなり大きな値になってしまいます。
以上及び、通常は周波数一致は成立させることは困難という現実的な理由により、一般的にはFDSは振幅スペクトルに対しては有効ではありません。
(4-3-3)FDSを適用した場合の周波数解像度
FDSを適用した場合はその結果のPSDの周波数解像度も変わったと解釈する方が妥当と考えられます。これは前述したように平滑化巾nのFDSは単純なn個のビンの移動平均ですので、FDSを適用すると周波数解像度は元の周波数解像度の1/nに、ビンの周波数巾はn倍になると解釈できるからです。例として式(25)に示した平滑化巾5のFDSの結果を考えると、ビンの周波数巾は元の5倍として、Po(0) (Pi(0)〜Pi(2)を使用)、Po(5) (Pi(3)〜Pi(7)を使用)、Po(10) (Pi(8)〜Pi(12)を使用)、..、Po(5xk; k=任意の正の整数)のみを採用し、他のPoはすべて無視、またはPo(2) ( Pi(0)〜Pi(4)を使用)、Po(7) (Pi(5)〜Pi(9)を使用)、Po(12) (Pi(10)〜Pi(14)を使用)、...、 Po(5xk-3; k=任意の正の整数)のみを採用し、他のPoはすべて無視しても構わないと考えられます。このようにすることによりFDSを適用した場合にPSDの値は小さくなりますが、各ビンの周波数巾が広くなるので、PSDと周波数巾をかけた例えば信号ビンの分散は変わらない、すなわち信号ビンに含まれる変動のエネルギー(又はパワー)は変わらないことになります。ただし、このような間引きをしなくても各ビンの周波数幅を変えなければ式(1)は満足されます。間引きを行った場合はビンの周波数巾も変えないと式(1)は成立しません。
本小額定型計算業務PD001シリーズではFDSを適用した結果にこのような間引きは行いませんが、その理由は表2A等に示す結果ファイルの列数をケースによって変更すると単純なテキストファイルでは実現困難になることと、Po(1)やPo(2)といった中間の値は内挿した値として使用できるので便利と思われるからです。
(4-3-4)FDSに代わる他の平滑化法
FDSに代わる周波数領域でのPSDの平滑化法としては(4-2-5)で記述したウェルチの方法も広く使われています。ただし、この方法を使用するとデータの数が元のものより小さくなりますので、ビンの数が減り、それに伴い自動的にビンの周波数巾は広くなります。現在は本小額定型計算業務PD001シリーズにウェルチの方法を加える予定はありませんが、お客様からのご要望が多い場合は別の小額定型計算業務として提供致します。
補足1 コンピュータを用いて計算をする際に生じる誤差について
コンピュータを用いて計算を行う場合、コンピュータは計算を進めていく過程で数値を保持するために決められたサイズのメモリを割当てていきますが、このために与えられたサイズのメモリでは収まりきれない桁数を持つ数(例えば1/3の結果のように無限の桁が必要な数)はある桁以下は省略されてしまいます。そして本来の値とは少し違う値を用いて計算を繰り返すうち、図2-5(a)や図2-18(b)でみられるほどの誤差が生じます。このデモンストレーションとして、いま仮に数字の桁数が4桁しか保持できないコンピュータがあるとし、この仮想的なコンピュータで(1/3-0.33)x100という計算をしてみます。まず、括弧内の最初の1/3の計算結果は0.3333(この仮想的なコンピュータは4桁しか保持できません)になります。次にこの値から0.33=0.3300を引くと0.0033になります。最後に括弧の外の100を掛けると0.3300=0.33になり、これがこの仮想的なコンピュータで数式とおりに計算した場合の結果です。ここで、この計算式を(1/3-0.33)x100=(1/3-33/100)x100=(100-99)/300x100=1/300x100=1/3のように手計算で変形します。そして最後の計算1/3のみをこの仮想的なコンピュータで行うと1/3=0.3333となります。この結果と前の結果を比べると、前の計算では有効な桁数が2桁になってしまっていて、結果として0.0033の誤差が生じたことがわかります。当事業所で使用しているコンピュータでは有効な桁数はおよそ(コンピュータは2進数で計算するので、10進数表現では”およそ”になります)16桁ですのでこの仮想的なコンピュータに比べれば遥かに正確な計算ができますが、それでも若干の計算誤差はほぼ常に生じてしまいます。したがって図2-5(a)の赤や紫の線で信号ビン以外の周波数で見られる非常に小さな値は実際はゼロであると見なすのが適当です。
補足2 パワースペクトル密度関数のスペクトル漏れと窓関数の関係について
(2-1-3-3)では周波数一致が成立しない場合は信号を本来の信号の周波数と異なる周波数の変動に式(3)に従い分解させることになるのでスペクトル漏れが発生すると記述しました。その事自体は誤りではないのですが、それではそもそも周波数一致が成立しない場合に式(3)のような形に分解する事が妥当かどうかという疑問が生じてしまいます。これに対し(4-2-1)では通常のPSDの計算においては手持ちの有限の長さのデータはそれが無限に繰り返される無限に長いデータの一部という仮定をおくことになり、結果として手持ちのデータの終了点と開始点が繋がれるが周波数一致が成立しない場合はそこで”崖”ができるためスペクトル漏れが発生すると記述しました。この記述も誤りでは無いのですが、この説明を基にしていてはスペクトル漏れの大きさを見積もる事は困難で、また窓関数を適用して”崖”をなくしてもスペクトル漏れはなくならないことがうまく説明できません。
そこでこの補足では手持ちの有限長のデータについて(4-2-1)とは異なる仮定をおくことにより、スペクトル漏れが起きるメカニズムを数学的により厳密に示した上で、スペクトル漏れの大きさを具体的に計算し、最後にスペクトル漏れを少なくする方法について記述します。なお、結論を先に書きますとスペクトル漏れが起きる原因は手持ちのデータの長さが有限であることです。
(1)データ長が有限であることの解釈及びこの補説で使用する変数の導入
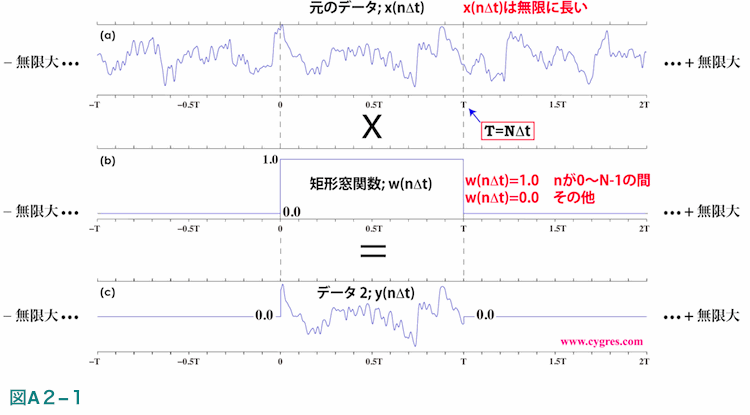
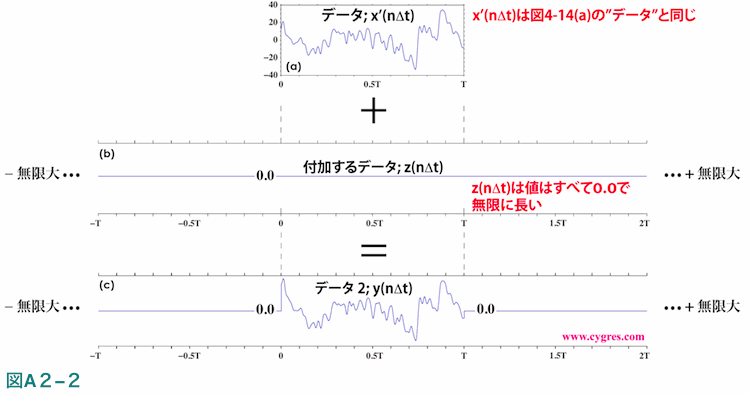
ここでは最初に手持ちの有限長のデータは図A2-1(a)の破線で区切られた区間に示すように無限に長いデータの一部と仮定します。
この仮定は(4-2-1)で記述したデータが無限に繰り返されるという仮定とはまったく異なり、元のデータはただ単に無限に長いだけで手持ちのデータの内容が繰り返す必要はないという仮定です。次にこの無限に長いデータに値が図A2-1(b)に示すように0からT迄の一定区間だけ1.0で他はすべて0.0というような矩形窓関数を適用します。その結果は図A2-1(c)に示すように0からT迄の間だけは元のデータの値と同じでそれ以外の値はすべて0.0というデータができますが、これを以下ではデータ2と称します。ここで重要なのはこのデータ2の長さは無限大で、そのため後に示すようにPSDのように一定間隔の周波数のみにおける値ではなく、PSDに類似した変数が連続した周波数において計算できる点です。なお、この段階で元のデータについては0からT迄の間の値のみ必要で、それ以外の点はどのような値でもよくなります。以下では矩形窓関数の値が1.0である巾を矩形窓関数の巾と称します。
次にここで生成された無限長のデータ2とまったく同じデータが手持ちの有限長のデータより作成できることを示します。図A2-2(a)を手持ちの有限長のデータとし、これに図A2-2(b)に示すデータ長は無限大ですが値はすべて0.0のデータzを足し合わせます。その結果としてできるのが図A2-2(c)に示すデータ2ですが、これは図A2-1(c)に示すデータ2とまったく同じです。
ここで値がゼロのデータzを手持ちのデータに加えるという操作は(2-1-3-3)で記述したゼロパッディングに相当し、データzの値はすべてゼロであるため、これを加えられたデータ2のスペクトルは元の図A2-2(a)のデータのスペクトル(厳密にはフーリエ変換結果)と変わりません。ただしデータ長が無限になるためデータ長に反比例するPSDのビンの周波数巾は無限小、すなわち0となり、今迄のように一定周波数間隔(離散)のPSDは計算できなくなります。
これらの2つの結果を纏めると、手持ちの有限長のデータ(図A2-2(a))のスペクトルというのは本来無限長のデータに有限の巾を持った矩形窓関数を適用したデータ2(図A2-1(c))のスペクトルと同じということになり、今迄”窓関数非適用”と称していた結果は実はデータ長の長い元データに対し手持ちのデータ長と同じ範囲だけ値が1.0である矩形窓関数を適用した結果であるという解釈ができます。したがって元のデータは無限の長さとし、それに対し適用する矩形窓関数の巾(図A2-2(a)データ長に相当)を変えるとどのように矩形窓関数が適用されたデータ(図A2-1(c)及び図A2-2(c)に相当)のスペクトルが変化するのかを調べれば、2章で記述したスペクトル漏れの原因などがわかると考えることができます。以下では”窓関数非適用”のPSDは矩形窓関数を適用したPSDと見なします。
ここで上に記述したようにデータが無限長の場合は式(19)に示したPSDはデータ長Tが無限大となるため計算できないので、PSDに類似したPSという変数を導入します。まず最初にフーリエ変換を示す式(18)の加算範囲を以下のように変更します。

次に図A2-1(b)で示した矩形窓関数を式(A2-1)のxmに適用した場合は式(A2-1)は
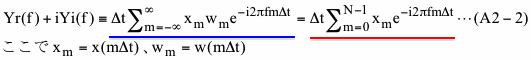
のようになります。この式の青下線部から赤下線部への移行の際には窓関数wmがmが0からN-1の間は1.0で他はすべて0.0であることを利用しています。この赤下線部は式(18)と周波数に関する部分以外はまったく同じですが、周波数は上で記述したように任意の値を選べますので、周波数を式(18)と同じように通常PSDを計算する周波数とした場合は式(A2-2)の結果は式(18)とまったく同じになります。
最後にこのYrとYiを用いてPSを以下のように定義します。
![]()
このPSは式(19)のPSDと非常によく似ていますが、式(19)の分子にある係数2.0と分母にあるTがありません。係数2.0についてはこの補足では説明の都合上片側スペクトルではなく両側スペクトルを用いるので不要となり、Tで割らない理由は単にTが無限大であるという理由です。ここで式(A2-3)と式(19)の最も重要な差はこういった目につく差ではなく、式(A2-3)のPSは任意の周波数で計算可能、別の言い方をすれば周波数領域で連続した変数であるのに対し、式(19)のPSDは一定間隔の周波数でのみ計算できる、いわば周波数領域で離散した変数であるという点です。したがって式(A2-3)のfを通常PSDを計算する周波数に選び、Tを矩形窓関数の巾とし式(A2-3)をTで割った後に2を掛けた値は、式(A2-2)がその場合は式(18)とまったく同じになることもあり、PSDとまったく同じになります。PSとPSDのこの関係を後ほど利用します。
(2) スペクトル漏れが起きるメカニズム及び、スペクトル漏れの大きさについて
当事業所が取り扱うようなデータは通常は有限ですので、式(A2-1)を用いて無限長のデータのフーリエ変換を計算することはできませんが、(2-1-3-3)で使用したような数式で表現できる仮想的なデータについては式(A2-1)が数学的に計算できる場合があります。具体的には(2-1-3-3)のケース1で使用したデータは
![]()
のように表現できます。xがこの式で表現できる場合はxのフーリエ変換結果、すなわち、式(A2-1)の左辺の各項は

のようになります。この式(A2-5)より式(A2-4)で表わされるデータのフーリエ変換は実数部はすべての周波数でゼロ、虚数部はデータに含まれる変動と同じ周波数及びその負の周波数でのみ値を持ち、他の周波数ではすべてゼロになることがわかります。この結果及び(4-2-6)で記述した畳み込み定理を用いることにより式(A2-2)の青下線部はその右の赤下線部へ移行させる代わりに以下のように変形できます。
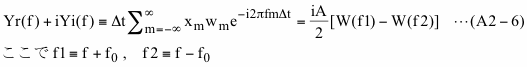
ここでW(f)は矩形窓関数の離散フーリエ変換で、以下のようになります。
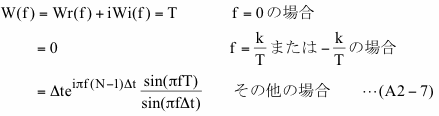
なお、上式の2段目のkは1以上N/2以下の整数で、3段目にも含まれます。
式(A2-6)は式(A2-4)で表わされる無限長のデータxに対し巾がT(データ個数ではN)の矩形窓関数を適用した場合のフーリエ変換になりますが、式(A2-5)で示されるxのフーリエ変換とは大きく異なり、窓関数に強く影響されることがわかります。この差が2章で示したスペクトル漏れの原因となります。式(A2-7)のWを実数部Wrと虚数部Wiに分けて式(A2-3)に代入すると、矩形窓関数を適用したデータのPSは以下のようになります。
![]()
では、次に上の数式(A2-8)で示されるPSが具体的にどのような形になるかを図を用いて示します。まず図A2-3(a)にここで使用するデータの時系列図を示します。
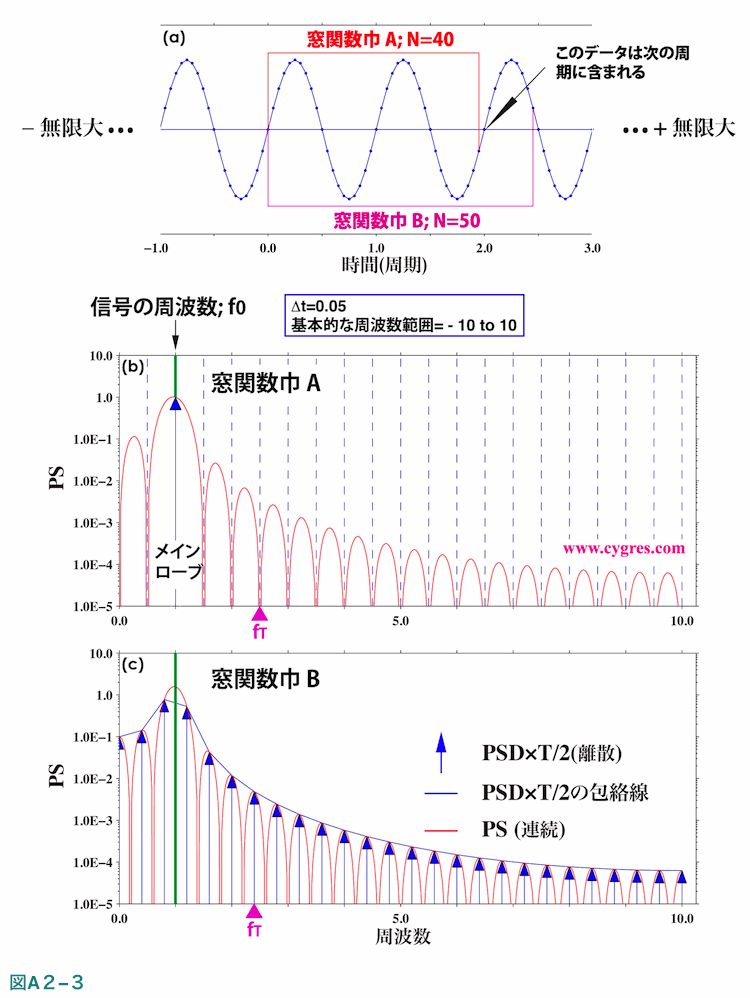
このデータは式(A2-4)と同じで、青線上の点が実際のデータです。矩形窓関数の巾はこの図中に赤及び紫で示した2ケースを用います。窓関数巾Aは図2-4ではデータ長Aに相当するケースで周波数一致が成立しています。このケースの場合、最後のデータは変動の2サイクル目が終了する1つ前の点のように見えますが、ここで扱うような離散データの場合はこの最後の点の次にある値が0.0になる点は3サイクル目の最初のデータになりますので、窓関数巾Aのケースは2サイクル分全体を含んでいることになります。なお、図中のNはデータの個数です。窓関数巾Bは図2-4ではデータ長Cに概ね相当するケースになります。なお、ここで使用するデータの個数は図2-4などに比べると遥かに少ないですが、これは以下で示す図を分かりやすくするためです。以下では変動の振幅(式(A2-4)中のA)は1.0にしています。またサンプリング間隔は0.05で、このため基本的な周波数範囲は-10から10になります。
図A2-3(b)の赤線は無限長のデータに巾Aの矩形窓関数を適用したと考えた場合(図A2-1(c)の”データ2”に相当)のPSを示します。前述したようにデータそのものは無限長ですので、PSは特定の周波数のみで与えられる離散値ではなく連続した値になります。この図では一定間隔で値が図の下端に達していますが、これらの点ではPSがゼロになっています。なおこの図は正の周波数領域のみ表示していますが、負の周波数領域についてはこの図の左端の周波数0.0を軸として反転させただけのものになるので省略しています。
図A2-3(b)の青の垂直の矢印はデータがデータ長Aの有限長のデータであると考えた場合( 図A2-2(a)の”データ”に相当)のPSDに定数をかけたものを示します。データ長Aは周波数一致が成立する場合になりますので、PSDは図2-5(a)の紫線(窓関数無)と同様に短い緑の垂直の実線で示す信号の周波数、すなわちf0と同じ周波数のビンでのみ値を持ち、他のビンの値はすべてゼロになり、その結果青矢印は一カ所だけにあるということになります。図中の青の縦の破線は他のビンの周波数を示しますが、これらの周波数は式(A2-6)のf1及びf2が1/Tの整数倍になりますので、式(A2-7)の2段目及び式(A2-6)よりPS(赤線)もゼロになります。なお、PSDに掛けられた定数はT/2で、この定数を掛ける事により式(A2-3)及び式(19)の比較でわかるようにPSとPSDの値が直接比較できるようになります。この図では青矢印の先端が赤の線(PS)に接していますが、これは偶然ではなく、前述したようにPSDと同じ周波数で計算したPSはここで使用したような定数をかけたPSDとまったく同じ値になるためです。
図A2-3(c)は窓関数巾もしくはデータ長がBの場合の結果を示します。この場合は上の例と異なりスペクトル漏れのために全てのビンでPSDの値がゼロではなくなり、定数をかけたPSDの各矢印の先端を結んだ青の実線(包絡線)は図2-6(c)の紫の実線で示すPSDと似た形になります。この図でも定数をかけたPSDの矢印の先端はそれぞれの周波数において赤の実線(PS)に接しています。図A2-3(b)及び図A2-3(c)よりスペクトル漏れは常に起きているが、周波数一致が成立している場合は信号ビン以外のPSDを計算する周波数ではPSがゼロになるためスペクトル漏れが生じていないように見えると考える事ができます。
その他、ややわかりにくいのですが、図A2-3(b)で示したメインローブはその中央に対して左右対称ではありません。この左右非対称性により(2-1-3-3)で記述したように周波数一致が成立しない場合は振幅スペクトルで最大の値を示すビンが信号ビンではなく、その隣のビンになる場合があります。
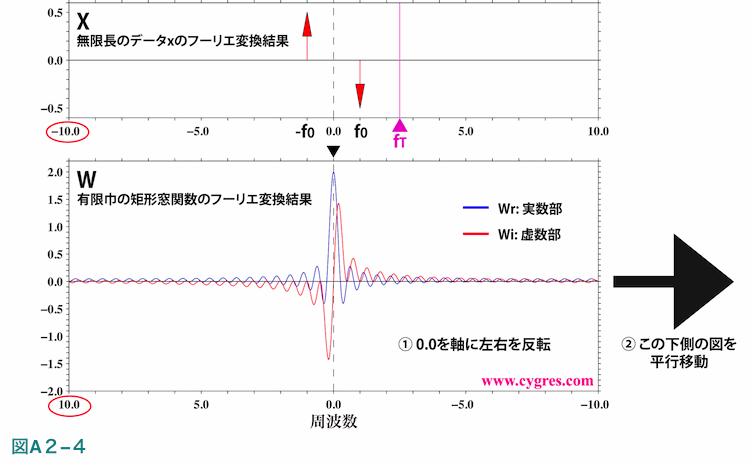
では、次にスペクトル漏れがどのようにおきるかを、畳み込みの操作を具体的に図化することによって示します。以下では図A2-3(b)及び(c)に紫色の三角で示した周波数fTをPSを計算する目的周波数として用います。図A2-4の上側の図は無限長データxのフーリエ変換Xで式(A2-5)を図化したものです。
Xは実数部はどの周波数でもゼロで、虚数部はf0及び-f0の2周波数でのみ値を持ち、他の周波数ではゼロになりますので、図では2個の赤色の矢印のみとなります。図A2-4の下側の図は巾がデータ長Aと一致する矩形窓関数のフーリエ変換Wで、式(A2-7)を図化したものです。こちらの方は、実数部、虚数部ともに連続した分布になるので矢印ではなく実線で表示しています。なお、式(A2-7)の2段目で示した特定の周波数では実数部、虚数部ともにゼロになります。XとWの周波数巾(図では横巾)は同じになりますが、これは両者の時系列値のサンプリング間隔が同じだからです。
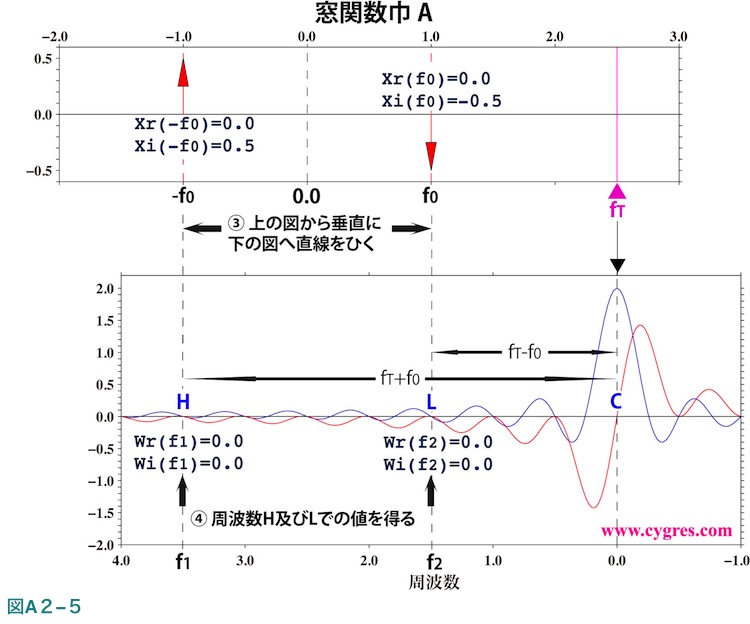
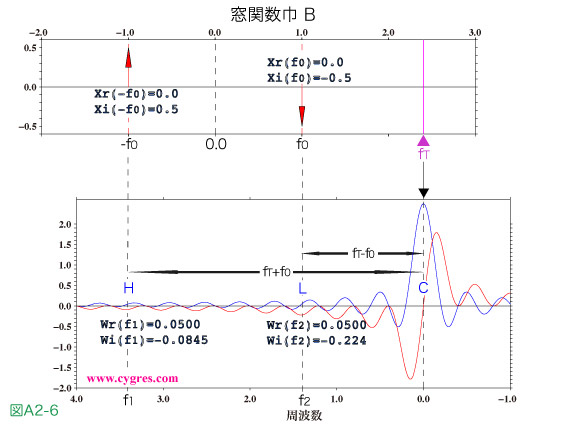
畳み込みの操作はまず最初に下側の図を水平軸の値が0.0の所を軸として左右反転させます。図ではこの操作は既に行なわれていますので、水平軸の左端の値(赤線で囲った値)は上側の図の右端の値と一緒になっています。次にこの下側の図を右方向に水平移動させ、上側の図の周波数fT(紫色の三角)と下側の図の中央にあたる周波数0.0(黒色の三角)の水平位置が同一になるようにします。矩形窓関数の巾がAの場合にこの操作の行なった結果を図A2-5に示します。
次に行なう事は上側の図で赤矢印が存在する周波数f0及び-f0から垂直に下側の図に線を引きます。これらの線は図A2-5では破線H及びLで表示していますが、破線Hと下側の図の周波数0.0(破線C)との周波数差はfT+f0、すなわちf1に(式A2-6)、破線Lと下側の図の周波数0.0との周波数差はfT-f0、すなわちf2になります。この際にもしf1が図A2-4で示す範囲を越えた場合は前述したフーリエ変換の周期性を利用します。
最後に下側の図の青線及び赤線が破線HおよびLと交わる点、すなわち周波数f1およびf2での値を読み、それらの値よりそれぞれの周波数でXとWを掛けた値
XW(f1)={Xr(-f0)Wr(f1)-Xi(-f0)Wi(f1)}+i{Xi(-f0)Wr(f1)+Xr(-f0)Wi(f1)}={-Wi(f1)/2}+i{Wr(f1)/2}
XW(f2)={Xr(f0)Wr(f2)-Xi(f0)Wi(f2)}+i{Xi(f0)Wr(f2)+Xr(f0)Wi(f2)}={Wi(f2)/2}+i{-Wr(f2)/2}
を計算し、その結果の合計を求めます。ここ迄の操作が畳み込みになります。ここでこの畳み込みを別の見方をすると、これは前述したようにWを重みとして周波数fTにおけるXの移動平均値(厳密には重みの総和は1.0ではないので、”平均”ではないのですが)を求めているのと類似になります。最後に畳み込みの結果を実数部と虚数部に分けて式(A2-3)に代入すると無限長のデータxに巾Aの矩形窓関数を適用したと考えた場合の周波数fTにおけるPSが求まります。
図A2-5で示すように矩形窓関数の巾がA、すなわち周波数一致が成立している場合は、fTがf0または-f0と同じ周波数のPSDのビン(信号ビン)以外のPSDのビンの周波数と一致すると、f1及びf2が常に1/Tの整数倍になりますので、上式のWr(f1)、Wi(f1) 、Wr(f2)及びWi(f2)は全て前述したようにゼロになります。従って式(A2-8)よりPSは信号ビンを除くPSDのビンの周波数では常にゼロになるためスペクトル漏れが生じないように見えます。しかしfTがこういった周波数より少しでも異なると、fTがf0もしくは-f0からどれだけ離れていようとも常にf0及び-f0にある信号を拾ってしまいます。
図A2-6は矩形窓関数の巾がBの場合ですが、この場合はfTがPSDのビンの周波数と一致してもWr(f1)、Wi(f1) 、Wr(f2)及びWi(f2)のいずれもゼロにならないためPSの値はゼロにならず、従ってPSDの値もゼロになりません。このようにして、周波数一致が成立しない場合はビンの周波数が信号の周波数よりどれだけ離れていても畳み込み、すなわち移動平均(前述のように厳密には重みの総和は1.0ではないので、”平均”ではないのですが)により信号を拾ってしまうためスペクトル漏れが生じます。式(A2-8)によればこのような場合の任意の周波数におけるスペクトル漏れの大きさは窓関数のフーリエ変換結果によって決まる事がわかります。図A2-4の下側の図で示すように矩形窓関数のフーリエ変換結果の値は周波数が変化するにつれ振動し、周波数がゼロから正負両方向に離れていくにつれ振動の振幅が減少します。この結果、周波数一致が成立しない場合はスペクトル漏れの大きさは目的とする周波数(fT)と信号の周波数(f0)が離れるにつれ小さくなる傾向があります。
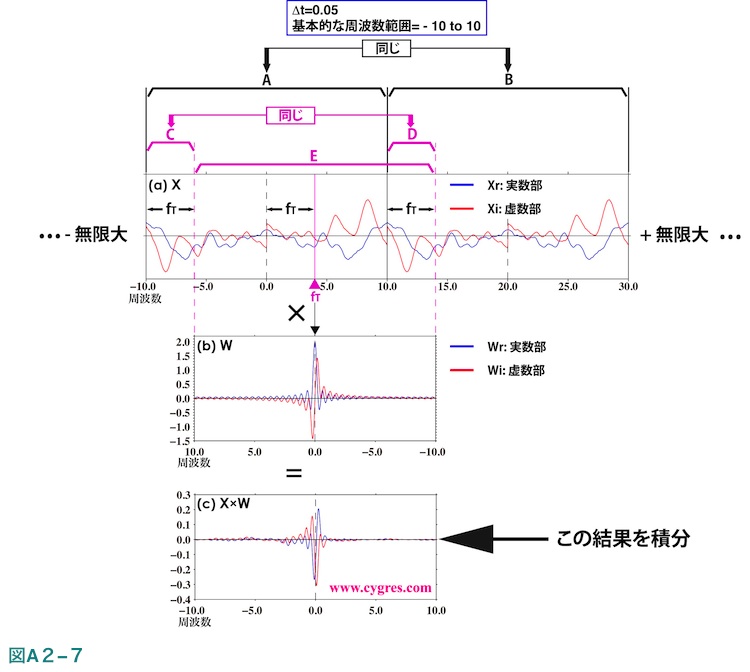
図A2-7に一般的な場合、すなわち無限長データxのフーリエ変換Xが上の例よりもっと複雑な場合、の畳み込みの過程を示します。
まず、図A2-7(a)はxのフーリエ変換Xを示します。この図では周波数ゼロを中心とした基本的な周波数巾(図では横巾)のセグメントAの右に同じ周波数巾を持つセグメントBも表示していますが、前述したXの周期性によりセグメントAとB内のXの値はまったく同じになります。ここで、前と同じく周波数fT(紫三角)におけるPSを計算したいと仮定します。図A2-7(b)は前と同じように矩形窓関数のフーリエ変換Wを左右反転させた後に中心周波数(黒三角)の水平位置がA2-7(a)のfT(紫三角)位置と一致するように平行移動させた結果を示します。畳み込みを行なうXの周波数範囲はこのWの両端の位置(紫破線)で囲まれるセグメントEになります。なお、セグメントEの周波数巾はセグメントAの周波数巾と同じです。このセグメントEをセグメントA及びBと比較すると、セグメントEにはセグメントAに含まれるセグメントCが欠けている反面、セグメントBに含まれるセグメントDが付加されていることがわかります。ここで、再びフーリエ変換の周期性を用いるとセグメントCとD内のXの値はまったく同じになりますので、セグメントEはXの基本周波数巾1周期分を過不足なく含んでいることになります。次のステップとしてXのセグメントEとWを掛けます。ここでの掛け算は図A2-5やA2-6と同様に図中で同じ水平位置にあるEとWの値を掛けていきますが、その結果を図A2-7(c)に示します。最後にこの結果を積分すれば式(A2-3)のYr(fT)及びYi(fT)が求められますので、それらの値を式(A2-3)に代入すれば周波数fTにおけるPSの値が求まります。この図より畳み込みはWを重みとしたXの移動平均と同様の形(厳密には重みの総和は1.0ではないので、”平均”ではないのですが)であり、移動平均の巾はXの基本的な周波数巾全域を含んでいるということがより明らかになります。したがってfTがどのような周波数であってもfTにおけるPSは、fTとの周波数差が式(A2-7)の2段目の周波数に該当するものを除き、X上に存在するすべての周波数の信号の影響を受けます。
(3)スペクトル漏れを少なくする方法
スペクトル漏れを少なくする現実的な方法は、データ長が有限であるがために意図しなくても適用されてしまう矩形窓関数の代わりに意図的にスペクトル漏れが少なくなるような窓関数を選択して適用するという方法です。 前述したようにデータの長さを無限にしたり周波数一致が成立するような長さに調節するとスペクトル漏れを防止できますが、実際のデータを取り扱う場合はどちらも現実的な対策とは言えません。
では、スペクトル漏れが少なくなる窓関数とはどのようなものかという点についてですが、前述したようにスペクトル漏れは窓関数のフーリエ変換結果の値によって決まるので、フーリエ変換結果の値が周波数ゼロ以外ではできるだけ小さな値になる窓関数がスペクトル漏れを小さくする窓関数ということになります。矩形窓関数に比べてスペクトル漏れを小さくする窓関数はいろいろありますが、ここではハニング窓関数を例として、矩形窓関数(窓関数非適用)との違いを記述します。なお、スペクトル漏れを完全に除去できる窓関数は無限長の巾(長さ)で値がすべて1.0という関数になり、窓関数の巾はデータ長と一致しなければなりませんので、このような窓関数を使用するという事はデータの長さを無限にするという事と同じになりますので、現実的ではありません。
式(A2-7)によって表わされる矩形窓関数の離散フーリエ変換に対しハニング窓関数の離散フーリエ変換は以下のようになります。

ここで、上式3段目のkは2以上N/2以下の整数で、式(A2-7)2段目のkと異なりkが1の場合は上式の2段目になります。
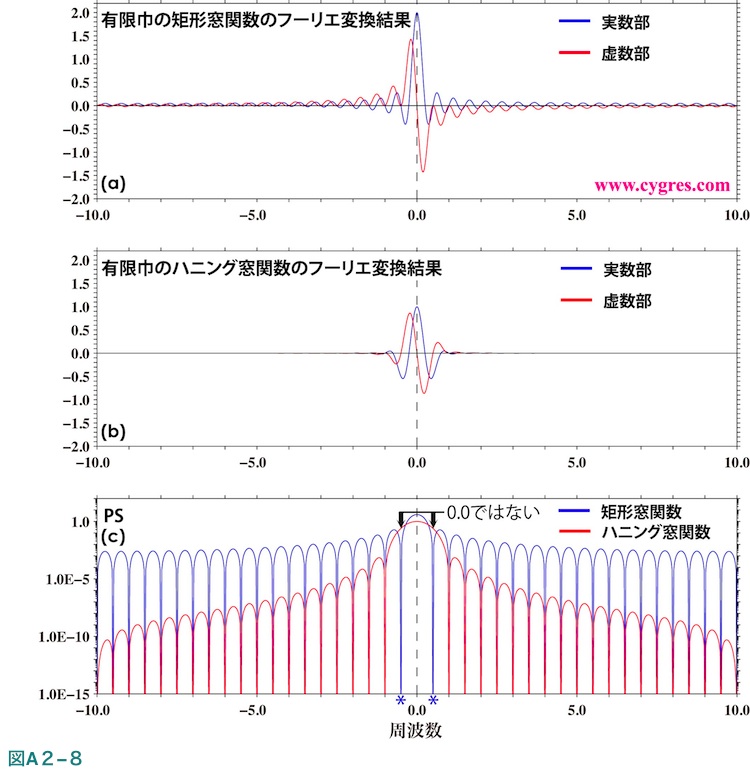
図A2-8(a)及び(b)に矩形窓関数及びハニング窓関数のフーリエ変換結果を示します。
図A2-8(a)では赤青両線とも周波数全域で視認できますが、図A2-8(b)ではおおよそ+/- 2.0より先ではどちらも見えなくなってしまいます。図 A2-8(c)はこれらの2つの窓関数のPSを対数スケールを用いて示しますが、この図よりハニング窓関数は矩形窓関数に比べるとスペクトル漏れをかなり減少させ、また両者の差は目的とする周波数(fT)と信号の周波数(f0)の差が大きくなるにつれ、大きくなることがわかります。また、この図よりハニング窓関数を適用することにより(4-2-1)で記述したような”崖”はなくなってもスペクトル漏れそのものは全周波数域で残ることがわかります。
なお、この図で青色の米記号で示した周波数においては矩形窓関数のPSはゼロになっていますが、ハニング窓関数のPSはゼロになっていません。また、周波数ゼロ(垂直の黒の破線)におけるハニング窓関数のPSの値は矩形窓関数のPSの値に比べ小さくなっています。これらにより(4-2-6)で記述したようにハニング窓関数を適用するとPSDの図では信号の巾が3ビンに広がります。ただし、ハニング窓関数を適用すると(4-2-3)で記述したような問題が生じる可能性もありますので、窓関数の選択はスペクトル漏れ以外の要素も考慮する必要があるかもしれません。