お問合せは
->こちらへ<-

パワースペクトル密度計算 (スペクトル解析)
小額定型計算 PD001A/B
小額定型計算業務はお取り扱いするデータの形式、計算内容、計算結果の内容及び形式やデータ授受方法といった業務全般を定型化することでコスト削減及び納期短縮を図った計算サービスです。科学、技術研究のみではなく、商業や工業のいろいろな分野のデータの解析にご利用下さい。小額定型計算業務については->こちら<-をクリック下さい。
図を含む本文書の著作権はCygnus Research Internationalに帰属します。無断転載はお断り致します。
PD001A/B ユーザーガイド 1/7
目次
(1章) PD001シリーズの要約
(1-1) PD001シリーズで行う計算について
(1-2) お客様がご指定できる計算設定項目の要約
(1-2-1) トレンド除去; 全てのケースで個別に指定
(1-2-2) PSDの値の信頼区間のパーセンテージ; 全ケースで同一の値を指定
(1-2-3) テューキー窓関数のテーパー比; ケースB1、B2及びB3のみ適用 値は個別に指定
(1-2-4) 周波数領域での平滑化(以下FDSと略)ビン巾; ケースA1、B1及びC1の3ケースを除く全ケースで 個別に指定
(1-3) 計算手法
(1-4) 入力データ(お客様のデータ)について
(1-5) プロダクツ
(1-5-1) 結果ファイル
(1-5-2) PDF形式の図
(1-6) 料金、納期およびご発注手順
(1-7) 個人情報、お客様のデータに関する情報保護
(2章) プロダクツの詳細及びその使用例
(2-1) 結果ファイル(本業務で納入するファイル)
(2-1-1) 結果ファイルのフォーマット(形式)
(2-1-2) 結果ファイルに記述する計算結果の内容
(2-1-2-1) 周波数 (Frequency)
(2-1-2-2) 周期 (Period)
(2-1-2-3) PSD (PSD)
(2-1-2-4) PSDの信頼区間 (Conf Int)
(2-1-2-5) 分散のパーセンテージ (% of Var)
(2-1-2-6) 振幅 (Amplitude)
(2-1-2-7) 位相 (Phase)
(2-1-3) 結果ファイルに書き出された情報の利用方法及び使用例
(2-1-3-1) 結果ファイルの値を用いて独自の図を作成したい場合
(2-1-3-2) PSD及びPSDの信頼区間の使用方法
(2-1-3-3) 特定の周波数での変動の巾(大きさ)を知りたい場合
(ケース1) 信号は振幅が一定の単一の周波数の三角関数で表される場合
(ケース2) 信号は振幅が一定の異なった周波数の三角関数を足し合わせたもので表される場合
(ケース3) 信号は単一の周波数の三角関数だが、振幅が時間とともに変動する場合
(ケース3-1) 信号の振幅の変動そのものが三角関数の形の場合
(例1) 信号は三角関数で周波数はf0。信号の振幅は周波数f1の三角関数の形で変動
(例2) 信号は三角関数で周波数はf0。信号の振幅は定数に周波数f1の三角関数を足し合わせた形で変動
(ケース3-2) 信号の振幅の変動そのものは三角関数ではない場合
(ケース4) 信号は周期的だが、三角関数の形ではない場合
(2-1-3-4) 特定の周波数域内の変動が全体の変動と比べてどの程度強いのかを知りたい場合
(2-1-3-5) 簡易デジタルフィルター(PD001Aのみ適用)
(2-1-3-6)データ中の値の変動の振幅を求める他の方法
(2-2)図
(3章) PD001シリーズ用のデータファイルの作成手順例
(4章) 各種指定項目の設定について
(4-1) トレンド除去;有無 無指定時は有
(4-1-1) トレンドとは? 除去の目的は?
(4-1-2) トレンド除去の例
(4-1-3) トレンド除去で問題が発生する例
(4-2) テューキー窓関数のテーパー比;%で表したテーパー比 無指定時は10%
(4-2-1) 窓関数を適用する理由
(4-2-2) 窓関数の適用とは
(4-2-3) ハニング窓関数;使用すると問題が生じる場合について
(4-2-4) 本小額定型計算業務 PD001Aでハニング窓関数を適用したPSDのみではなく、窓関数非適用及び テューキー窓関数を適用したPSDも計算する理由
(4-2-5) ハニング窓関数によるデータ両端近くの減衰を少なくする方法
(4-2-6) 窓関数が持つFDSに似た効果について
(4-2-7) IFDSは必ずしもPSDを平滑化しない
(4-2-8) 窓関数適用によるPSDや振幅スペクトル減衰に対する補正
(4-2-9) 窓関数適用時の補正の効果
(4-2-10) テューキー窓関数のテーパー比がPSDに与える影響
(4-3) 周波数領域での平滑化(FDS)ビン巾; 1、3、5、7等奇数 無指定時は無し(1)、3及び7
(4-3-1) PSDに対するFDS
(4-3-2) 振幅スペクトルに対するFDS
(4-3-3) FDSを適用した場合の周波数解像度
(4-3-4) FDSに代わる他の平滑化法
補足1 コンピュータを用いて計算をする際に生じる誤差について
補足2 パワースペクトル密度関数のスペクトル漏れと窓関数の関係について
補足3 データ長が短いと単一のピークが現れ、長いとツインピークが現れる理由
補足4 S1のトレンド除去により付加される直線成分のPSDの悪影響に対するS1とSRの周波数の関係
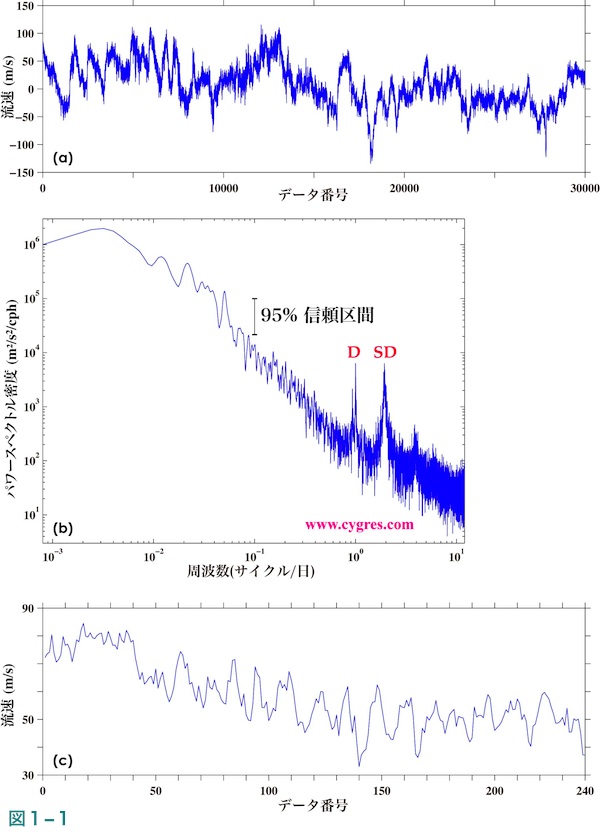
パワースペクトル密度関数(以下PSDと略)は、データ中に周期的な変動が存在する場合にその周期(あるいは周波数)や振幅を調べるためによく用いられます。例として図1-1(a)及び(b)に海洋の流速データの時系列及びそれより計算したPSDを示します。PSDの図(図1-1(b))では1日周期(図中でDと表示)及び半日周期(同SD)の潮汐成分の存在が容易にわかりますが、時系列の図(図1-1(a))ではこれらの変動があるかどうかはまったくわかりません。図1-1(c)は図1-1(a)の最初の240データのみを取り出して拡大した図で、この期間中に1日周期の潮汐は24回、半日周期の潮汐は48回あることになるのですが、この図でも両潮汐成分は明確ではありません。
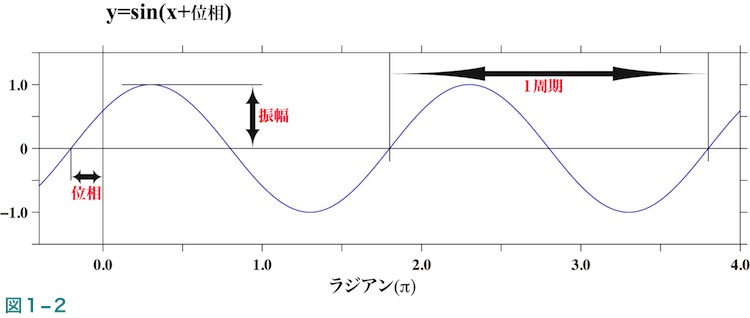
本小額定型計算業務PD001シリーズではお客様のデータの数値の変動を異なった周波数の三角関数に分解し、それらの振幅を計算することによってPSDを求めるという一般によく使われる方法を採用しています。図1-2に三角関数を示しますが、もしお客様のデータの変動に鋭い角、刺(スパイク)や階段状(矩形波を含む)といった変動がある場合は、それらの変動がたとえ非常に正確な周期を持っていても本業務で計算した結果の解釈にはやや注意が必要となる可能性があります。->ここ<-で色々なデータのPSD例を記述していますので、よろしければ御参照下さい。
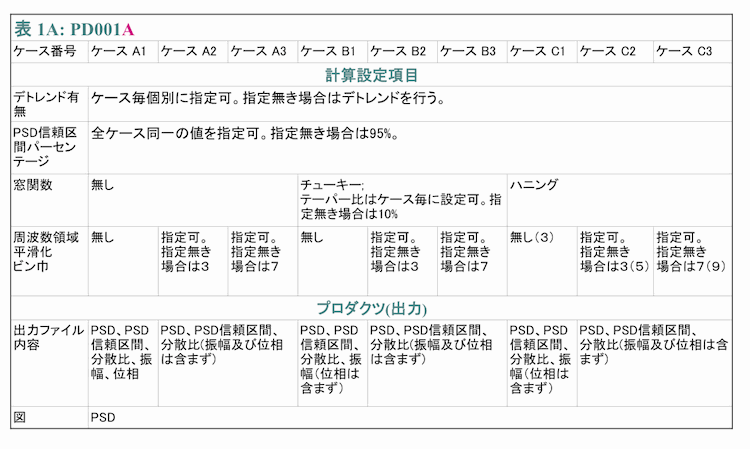
PSDを計算する際には事前に決めなければならない項目が幾つかありますが、大抵の場合は実際に計算を行ってその結果を調べてみなければそれらの設定が適切かどうかよくわからないのが現実です。そこでPD001Aでは下の表1Aに示すように1注文で9ケースの異なった設定で計算を行い、お客様の側でそれらの結果を比べた上でその中から最適な結果を選択して頂けるようにしています。ただし、PD001Bでは表1Bに示すように1注文で1ケーズの計算のみを行います。
以下では1章では価格を含む本業務の要約を、2章では計算結果を格納したファイルや図といった本業務のプロダクツの内容の詳細及びその利用例を、3章ではマイクロソフト社のエクセルを用いた入力データファイルの作製方法を、4章では本業務でお客様にご指定頂く各種設定についての解説を記述しています。1章の内容は簡潔なものとしていますが、詳細は2章以後に詳しく記述していますので、1章の内容でご不明な点があった場合は2章以後もお読み頂きますようお願い致します。
本文書では周波数と周期を適宜入れ換えて使う場合がありますが、周期は周波数の逆数(周期=1/周波数)で、例えば周波数が2サイクル/秒の場合の周期は1/2=0.5秒となり、周波数が高いと周期は短くなり、逆に周波数が低いと周期は長くなります。また、本文書では時間領域と周波数領域という言葉を用いていますが、これは図1-1のような場合に水平軸が時間なのか周波数なのかといったような違いで、図1-1(a)は時間領域でのデータの表示で、図1-1(b)はそれに対応する周波数領域でのデータの表示となります。本文書では時系列データを扱っていますが、もしお客様のデータが、例えば物質の色を直線に沿ってスキャンしたような何かの1次元の空間分布である場合は時間を空間に置き換えて下さいますようお願いします。
本文書はPSDの解説を目的としたものではなく、当時業所が提供する小額定型計算業務PD001シリーズの解説を目的としたものですので、数式や専門用語の使用はできるだけ避け、PSDの数学的に詳細な定義や導き方といった事よりは実際の計算結果がどのようなものになるのか、また実際の計算精度はどの程度かといった記述が中心となっています。また、一部の表現は数学や統計学的には厳密ではないことをあらかじめお断り致します。
(1章) PD001シリーズの要約
(1-1) PD001シリーズで行う計算について
PD001Aで行う計算の要約を表1Aに示します。PD001Aでは1回のご注文でこの表に示す9ケースすべての計算を行います。これに対しPD001Bでは表1Bに示すように1ケースの計算のみ行います。計算設定項目はお客様にご指定頂く項目で、トレンド除去の有無、PSDの信頼区間のパーセンテージ、窓関数及び周波数領域で行う平滑化の巾の4種類があり、これらの概要は(1-2)に、詳細は4章に記述しています。なお、窓関数はPSD計算前にデータに掛ける重み(係数)で現在はテューキー窓関数のテーパー比のみ指定可能となっています。
プロダクツはお客様にお渡しする計算結果です。なお、PD001Aでは位相についてはケースA1でのみ、振幅についてはケースA1、B1及びC1でのみ計算致します。これは位相や振幅については他のケースでは計算する意味が無いためで、その詳細については後述致します。PD001Bをご発注の場合も位相や振幅に関してはこれに準じます。計算結果を格納したファイルの各項目については2章に記述していますので、そちらをご参照お願い致します。なお、図についてはPD001Aをご発注の場合は各ケースのPSDの図をPDF形式でご提供致しますが、PD001Bをご発注の場合は図はご提供致しません。表1CにPD001AとPD001Bの差異を示します。
PD001シリーズで計算するPSDは片側PSDとなりますが、 片側PSDについては(2-1-2-3)に記述しています。 PSDが計算される周波数は、最低が0、最高が1/(2xサンプリング間隔)となり、各周波数間の間隔は一定で1/(サンプリング間隔xデータ数)となり、データ数/2+1点の周波数となります。なお、ここでサンプリング間隔というのはデータが取得された時間間隔です。例として、もしサンプリング間隔が5秒、データ数が200の場合は、PSDが計算される周波数は0サイクル/秒(0Hz)から1/(2x5)=1/10=0.1サイクル/秒(0.1Hz)でその間の周波数間隔は1/(5x200)=1/1000=0.001サイクル/秒(0.001Hz)となり、総計200/1+1=101周波数となります。
(1-2) お客様がご指定できる計算設定項目の要約
(1-2-1) トレンド除去; 全てのケースで個別に指定
PD001シリーズでは必要であれば最小自乗法を用いてデータを直線近似し、その直線成分をデータより除くというトレンド除去を行いますが、この作業を適用するかどうかの選択で、デフォルト(指定が無い場合の設定)は適用となります。通常は適用したほうが良いとされていますが、(4-1-3)で記述するような特別なケースでは問題が発生する可能性があります。トレンド除去の詳細は(4-1)に記述しています。
(1-2-2) PSDの値の信頼区間のパーセンテージ; 全ケースで同一の値を指定
0.0より大で100.0より小な値であればどのような値でも可能ですが、一般には80、85、90、95、99及び99.5%といった値がよく用いられていて、特別な理由が無い限りこれらの値の中から選択されることをお勧めいたします。なお、デフォルトは95%で、具体的な利用例については(2-1-3-2)に記述しています。この値についてはケース毎に異なる値を設定する必要は無いと思われますので、同一の値を全ケースに適用致します。
(1-2-3) テューキー窓関数のテーパー比; ケースB1、B2及びB3(PD001A)のみ適用 値は個別に指定
0.0より100.0の間であればどのような値でも可能ですが、0.0をご指定になると窓関数を適用しないのと同じ(PD001AのケースA1〜A3)になり、100.0をご指定になるとハニング窓関数を適用するのと同じ(PD001AのケースC1〜C3)になります。デフォルトは10.0となります。窓関数全般については(4-2)に、テューキー窓関数のテーパー比が計算結果にどのような影響を与えるかについては(4-2-10)に記述しています。
(1-2-4) 周波数領域での平滑化(以下FDSと略)ビン巾; ケースA1、B1及びC1の3ケースを除く全ケースで個別に指定
周波数領域で行う平滑化(以後FDSと略)のビン巾というのはPSD計算後に適用する重み無しの移動平均の巾で、詳細については(4-3)に記述しています。1以上データ数/2+1以下の奇数の整数であればどのような値でも可能ですが、1をご指定になると平滑化を行わないのと同じになります。デフォルト値は表中に示した値となりますが、ハニング窓関数を使用した場合は、ハニング窓関数自体に平滑化に準じた効果が含まれていますので実際の平滑化の巾は指定値より広くなり、おおよその巾は表中の括弧の中のような値になります。
(1-3) 計算手法
PD001シリーズでは通常よく用いられる方法でPSDを計算致します。計算手順は最初にご指定があればデータよりトレンドを除き、次に必要であれば窓関数を適用し、その後にFFTという方法を用いてPSD及び振幅スペクトルを計算致します。窓関数を適用した場合はこの後補正を行い、さらにFDSが必要な場合はFDSを適用致します。最後に分散比を計算致します。
(1-4) 入力データ(お客様のデータ)について
PD001シリーズでお取り扱いできるデータのファイルはいわゆるテキストファイルで、ファイル内には半角の数値及び数値間の区切りとして半角のスペースまたはコンマのみを含むのものとなります。数値の表示方式については-123.4のような通常の形式でも-1.234E2のような指数表示でも結構です。入力データのファイルの内容の具体例については図3-5を参照頂きますようお願い致します。全角の数値やスペース、コンマを含むファイルは前処理が必要となり、その料金は別途加算となります。バイナリーのデータやデータが複雑な方式や順序で記録されているアスキーコードのデータのような場合は当事業所で変換用のプログラムを作成して処理することになりますが、その場合についても別途処理料金が発生します。ただし、新規にプログラムを作成しなければならないような場合はPD001Aの料金の数倍から数十倍の追加料金が発生する可能性もあることをあらかじめお断り致します。追加料金のお見積もりは無料です。なお、入力データのファイルをマイクロソフト社のエクセルを用いて作成する例は3章に記述しています。
その他の条件としては、データのサンプリング間隔は一定でなければなりません。サンプリング間隔が一定ではない場合は当事業所で適当な内挿方法を用いてサンプリング間隔を一定としたデータを作成することも可能ですが、その場合は別途料金が加算となります。なお、データの個数については100万程度でも処理可能ですが、奇数個の場合はこちらで値が0のデータを1個付加し偶数個にしてから処理を行います。この方法はゼロパディングと呼ばれ、計算の精度等には影響を与えません。この作業については追加料金は発生致しません。
PD001シリーズではお客様のデータのチェックは基本的には行いません。したがいまして、御発注前にお客様の側でデータが適切なものかどうかを図1-1(a)のような時系列図を作成してチェックされることをお勧めいたします。もしお客様のデータに異常な値が含まれている場合、当事業所でそれらの異常な値を検出しそれらの値を無効データとして周辺の値より内挿して置き換えるような処理も可能ですが、その場合は異常な値の明確な定義が必要となり、また別途加算料金が発生いたします。なお、データの数値の単位をご連絡頂いた場合はPD001Aで作成する図のラベル等に使用致します。単位が不明な場合は図のラベルの単位は無記入となります。
御見積もりは無料ですので、データファイルがここや3章でご説明するような形式でない場合や異常な値の検出その他の前処理が必要な場合の追加料金については事前にお問い合わせ頂きますようお願い致します。
(1-5) プロダクツ
PD001Aでは表1Aに示したようにPSDその他の計算結果を格納したファイル(以後”結果ファイル”と称します)及びPSDのPDF形式による図を提供致します。PD001Bをご発注の場合は表1Bに示すように結果ファイルの提供のみ行います。
(1-5-1) 結果ファイル
結果ファイルはいわゆるアスキーコードのテキストファイルで、半角の英数字及び数値間の区切りとして半角のコンマのみを含みます。このファイルの詳細については2章に記述しますが、このファイルの最初の行はヘッダーに該当するもので、2行目以後の各列の説明が英文で記述されています。2行目以後は数値及びその区切りのコンマのみを含みます。このファイルはマイクロソフト社のエクセルのcsv形式とよばれる形式と同じですので、このファイルの拡張子をcsvとしています。お客様ご使用のパソコンにエクセルをインストールされている場合は、csvファイルをエクセル以外で開くように設定されていない限り、通常はこのファイルをダブルクリックすればエクセルが起動されて自動的にエクセルに読込まれます。ただし、結果ファイルは基本的には単純なテキストファイルですので、エクセル以外でも普通のテキストエディターなどで内容を閲覧することが可能です。なお、アスキーコードのファイルの各行の終端のコード(復帰、復帰改行、改行コード)はOSがWindows、旧MacOS又はLinuxかによってすべて異なりますが、PD001シリーズではWindowsの形式を採用しています。大抵のソフトウェアは行の終端コードの違いを自動的に判別して対応しているようですが、マイクロソフト社のOSに標準装備されている”メモ帳”などの場合はWindows以外の終端コードのファイルは改行が行われず全行一続きで表示されてしまいます。他社のOSについても同じようなアプリケーションがあるものと推定されますので、他社のOSを使用されている場合はご注意ください。
(1-5-2) PDF形式の図
PD001Aをご発注の場合は表1Aに示したように全ケースのPSDの図をPDF形式で提供致します。図の詳細については(2-2)に記述しますが、1ファイルにつき1ケースの図となります。PD001Bをご発注の場合は図の提供は致しません。
(1-6) 料金、納期およびご発注手順
PD001Aの料金は1データセット(個々のデータファイル内にあるデータの個数ではありません)につき2300円(税込み、Paypal社手数料込み)となります。もし複数のデータセットの処理をご要望の場合は2セット目より1セット当たり1000円(税込み)加算となります。例として3データセット処理する場合の料金は2300+1000x2=4300円となります。なお、複数データセットの処理料金に対する割引は同時にご発注頂いた場合のみで、個別に3セットの処理をご発注されますと2300x3=6900円となります。
PD001Bの料金は1データセットにつき1200円(税込み、Paypal社手数料込み)となります。もし複数のデータセットの処理をご要望の場合は2セット目より1セット当たり600円(税込み)加算となります。なお、複数データセットの処理料金に対する割引は同時にご発注頂いた場合のみ適用いたします。
納期は処理するデータセットの数(個々のデータセットに含まれるデータ数ではありません)にもよりますが、通常はご発注確定後1-2営業日程度となります。なお、ご発注確定は以下の手順では(手順4)に該当致します。
ご発注手順は以下のとおりとなります。
(手順1)まず、当事業所にご発注の意図があることをメールでご連絡下さい。その際にはデータセットの個数もご連絡頂きますようお願い致します。メールの送付先は->ここ<-をクリック下さい。
(手順2)上でご連絡を頂きますと当事業所でスケジュールの確認を行い、可能な納期を可及的すみやかにメールにてご連絡いたしますので、その納期でよいかどうかご検討お願い致します。
(手順3)上で発注を決められた場合は再度メールにてご発注お願い致します。なお、その際にはデータファイルを添付下さい。
(手順4)上で送付頂いたメールを当事業所で受け取った場合はその旨メールにてご連絡し、データが処理可能可能かどうかの簡単なチェック(ファイルの形式のみ;値のチェックは行いません)の後、作業を開始致します。
(手順5)当事業所で作業を完了致しますと、作業完了の証明としてPD001Aをご発注の場合は表1Aのケース1に該当するPSDの図をjpeg形式(PDFではありません)にしたものを添付してメールにてご連絡いたします。なお、PD001Bをご発注の場合にお送りする作業完了証明用のPSDの図は全周波数域の低域側半分のみ含むものとなります。
(手順6)こちらからお送りした図をご確認後、料金をpaypal社経由にてこの->ページ<-でお支払い頂きますようお願い致します。なお、お客様とpaypal社とのお取り引きの際のクレジットカード情報などは当事業所には一切伝達されません。
(手順7)当事業所でお客様のpaypal社経由でのお支払が確認できましたら、結果ファイル及び正式な図(PD001Aのみ)をメール添付にてお送り致します。なお、当事業所ではお客様のデータおよびPD001シリーズの結果ファイルは保存致しませんので、ご注意お願い致します。
データの送受をメール添付以外の方法で行うことは可能ですが、別途作業料金および送料等の実費が加算となります。
(1-7) 個人情報、お客様のデータに関する情報保護
当事業所はお客様の個人情報やお客様のデータに関する情報については以下のいずれかの条件を満たさない場合は第三者には提示いたしません。
条件(1)お客様の同意もしくは指示があった場合
条件(2)裁判所その他の日本国内の司法機関より法律に基づく命令があった場合(要請は本条件を満たしません)
お客様のデータおよびPD001シリーズの計算結果は業務完了後1週間程度で削除致しますので、PD001シリーズの計算結果はお客様の側で保管頂きますようお願い致します。なお、業務完了日時はお客様のお支払いが確認できた日時となります。業務管理のためお客様のメールアドレス、ご発注日時、業務完了日時及びPD001シリーズの制御用ファイルは保管致しますが、この制御用ファイルにはお客様のデータは一切含まれません。
(2章) プロダクツの詳細及びその使用例
この章以後では文章のみでは説明が非常に複雑になるような場合に数式を使用致しますが、その際に以下の様な数学記号を用いています。

(2-1) 結果ファイル(本業務で納入するファイル)
結果ファイルは前述したように半角英数字のみを含むいわゆるテキストファイルです。
(2-1-1) 結果ファイルのフォーマット(形式)
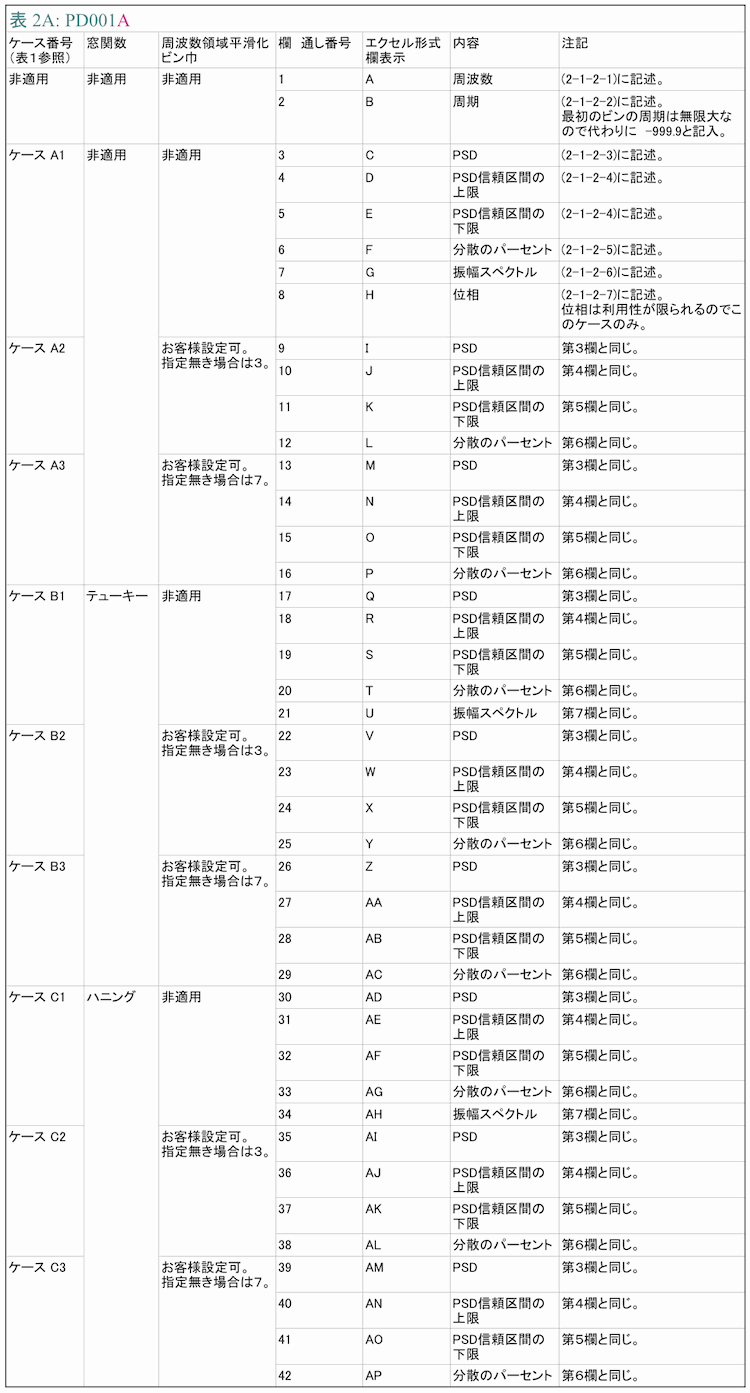
計算結果を格納したファイルの第一行目はヘッダーに該当する行で、この行に2行目及びそれ以後の行の各列の数値の意味を記述しています。なお、ヘッダー行では以下(2-1-2-1)から(2-1-2-7)の各節冒頭の括弧内に示した英表記を使用しています。2行目及びそれ以後は実際の計算結果で、データ数/2+1行あり1行につき特定の1周波数(周期)の計算結果を書き出しています。表2AにPD001Aをご発注の場合について、表2BにPD001Bをご発注の場合について2行目以後の各行に記述する計算結果の内容の一覧を欄別に示します。計算結果の詳細は以下の(2-1-2-1)から(2-1-2-7)に記述しています。なお、数値は-1.234E-5のようにすべて指数表示になっていて、数値間の区切りはコンマを使用しています。
(2-1-2) 結果ファイルに記述する計算結果の内容
以下(2-1-2-1)から(2-1-2-7)迄の各節冒頭の括弧中の名前は結果ファイル1行目のヘッダー行で使用している名前です。
(2-1-2-1) 周波数 (Frequency)
PSDその他の値は前述したように0から1/(2xサンプリング間隔)迄の1/(サンプリング間隔xデータ数)間隔の周波数で計算されますが、結果ファイルに書き出される周波数はこれらの周波数です。なお、最高周波数や周波数間隔はサンプリング間隔やデータ数で自動的に決定され、任意の値を選ぶことはできません。前述したように、もしサンプリング間隔が5秒、データ数が200の場合は、PSDが計算される周波数は0サイクル/秒(0Hz)から1/(2x5)=1/10=0.1サイクル/秒(0.1Hz)で、その間の周波数間隔は1/(5x200)=1/1000=0.001サイクル/秒(0.001Hz)となり、2行目からの行数は200/1+1=101行となります。
周波数の単位はサンプリング間隔の単位によって決まります。例えば、サンプリング間隔が2日である場合の周波数の単位はサイクル/日です。周波数の単位をサンプリング間隔の単位と異なるものにしたい場合(前の例で周波数の単位をサイクル/秒に変更等)は発注時に明記下さいますようお願い致します。なお、サンプリング間隔をご連絡頂かない場合はサンプリング間隔は単位無しの1.0とみなし、周波数の単位はサイクル/単位無しの1.0となります。
一般にPD001シリーズのように一定周波数間隔でPSDを計算する場合、計算されたPSDはPSDが計算された周波数を中心に一定の周波数巾を持つ領域のPSDを表わすものという考え方をする事が多くあります。この周波数領域は通常ビンと呼ばれ、ビンの周波数巾はPSDの周波数間隔と同じです。上の例を用いると3番目のビンの中心周波数は0+((3-1)x周波数間隔)=2x0.001=0.002サイクル/秒で、このビンの周波数の下限は中心周波数 ー(周波数間隔/2)=0.002-(0.001/2)=0.002-0.0005=0.0015サイクル/秒で、上限は中心周波数 +(周波数間隔/2)=0.002+0.0005=0.0025サイクル/秒となります。本ドキュメントではこのビンの概念を所々で使用致します。ただし、ここで1つ注意しなければならない点はPSDや振幅スペクトルそのものはあくまでもこの結果ファイルに書き出される周波数において計算された値であって、各ビンに含まれる周波数域の平均のようなものではありません。
(2-1-2-2) 周期 (Period)
周期は周波数の逆数(周期=1/周波数)です。最初のビン(結果ファイルの第2行目)の周期は周波数がゼロなので無限大になりますが、そのような値は書込めないので-999.9としています。この第2行目を除けば周期は常に正の値で、単位はサンプリング間隔の単位と同じになります。
(2-1-2-3) PSD (PSD)
PSDには片側PSDと両側PSDがあり、両者ともに広く使用されています。両側PSDは正負両側の周波数で定義され、周波数ゼロを中心として値の分布は対称となります。例えばある正の周波数fでのPSDは負の周波数-fでのPSDと同じ値です。これに対し片側PSDは正の周波数でのみ定義され、値は周波数ゼロおよび最高周波数のものを除くと両側PSDの値の2倍になります。PD001シリーズで結果ファイルに書き出すPSDは片側PSDです。なお、PSD計算時に窓関数を適用した場合は計算されたPSDに対し補正を行っていますが、補正の詳細は(4-2-8)に記述しています。PSDの単位はお客様のデータの単位の自乗を周波数の単位で割ったものになります。
(2-1-2-4) PSDの信頼区間 (Conf Int)
PD001シリーズではPSDの信頼区間は通常よく使われる方法で計算していますが、これは平均値の信頼区間(->ここ<-に記述しています)と似たような概念に基づいています。PSDの信頼区間の具体的な使用例は(2-1-3-2)に記述しています。
(2-1-2-5) 分散のパーセンテージ (% of Var)
まず分散に関してですが、分散はデータの値の変動のパワーもしくはエネルギーといったようなものに関連しています。例えば自動車の運動エネルギーはその自動車の質量にスピードの自乗をかけたものを2で割った値であり、あるモータが消費する電力(パワー)はそのモータに流れる電流の自乗にモータ自体の抵抗値を掛けた値になるように、一般にエネルギーやパワーはある値の自乗に比例します。平均値の除去を行ったデータの分散はデータ中のそれぞれの値の自乗の平均値になりますが、この値の自乗という点で運動エネルギーなどと類似点があるのでデータ自体はエネルギーやパワーにはまるで関係がないと思われるようなもの(例えば株価)であっても分散は変動の大きさあるいは”パワー”を表わすと考えることができます。なお、周波数領域の値であるPSDは時間領域の値である分散に対応するといった関係が両者の間にあります。
あるビンのPSDにビンの周波数巾(ビンによらず一定の値です)を掛けた値はそのビンに含まれる分散になり、周波数ゼロを除くすべてのビンの分散を足し合わせた値は平均値を除去したデータの通常の分散と同じになります。これを数式で表現すると

まれていません。この周波数ゼロのビンのPSDはデータの変動には無関係で、データより平均を除去した場合はゼロ(実際には計算過程の誤差のため非常に小さな値)となり、除去しなかった場合はデータの平均値の自乗にデータ長をかけたものとなります。
この式により、あるビンのPSDにビンの周波数巾をかけた値を時系列データの分散で割った値は、そのビン内の変動が全体の変動のどの程度を含むかを示します。これにさらに100を掛けたものが分散のパーセンテージで、これを数式で表現すると
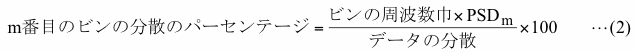
となります。
(2-1-2-6) 振幅 (Amplitude)
PSDの計算においてはお客様のデータの数値は異なる周波数の三角関数の和としてとらえます。これを数式で表現しますと
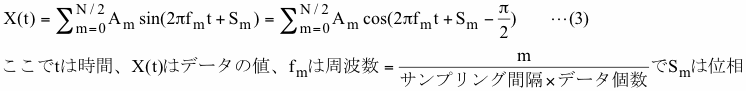
結果ファイルに書き出される振幅はこの式中のAmで、図1-2に示すように上側のピークから下側のピークまでの巾の半分です。なお、Amそのものは時間によらない定数となります。振幅の単位はデータの単位と同じで、この値により特定の周波数における変動の振幅がわかることになります。
PSD計算時に窓関数を適用した場合は計算された振幅に対し補正を行いますが、(4-2-8)の記述のように振幅に対する補正はPSDに対して行う補正と少し異なります。このため窓関数を適用しない場合については振幅はPSDの2倍に周波数巾をかけたものの平方根と等しくなりますが、窓関数を適用した場合はその関係が成り立ちません。なお、振幅に対してFDSを適用すると無意味な結果にしかなりませんので、表1Aや表1Bに示すようにFDSを適用したケースについては振幅は結果ファイルには書き出しませんが、これについての詳細は(4-3-2)に記述しています。
(2-1-2-7) 位相 (Phase)
位相は上の数式(3)でのSmに該当します。位相は通常のPSDの計算では無視されることが多いのですが、まったく有用性がないというわけではありません。具体的な使用例としては、(2-1-3-5)に記述するように特定の周波数の振幅及び位相のみを数式(3)に代入することにより、元のデータ中の特定の周波数範囲の変動のみを含む時系列データを作成することができます。ただ、一般的にはそれ以外の用途はないようですので、PD001Aをご発注の場合は表1Aに示すようにケースA1以外のケースについては位相は結果ファイルには書き出しません。PD001Bをご発注の場合も同様です。なお、位相の単位はラジアンで、度ではありません。
(2-1-3) 結果ファイルに書き出された情報の利用方法及び使用例
(2-1-3-1) 結果ファイルの値を用いて独自の図を作成したい場合
当事業所では出版物の原稿としても使用可能なポストスクリプト形式の図の作成作業も承りますが、料金は一般的には図1枚に付きPD001Aの料金と同等かそれ以上となります。単にPD001シリーズの計算結果を調べるという目的だけであればお客様ご自身がエクセル等を用いて作図されるほうが便利と思われますので、この章では作図に関する必要事項等を簡単に記述致します。ただし、エクセルを使用しての具体的な作図方法などはインターネットで容易に多くの情報が得られますのでここでは割愛致します(”エクセル グラフ 作成”の3語でネット検索を行っていただければ多数の情報が得られます)。
ここでは、すべてデフォルト設定でPD001Aによって計算を行い、その結果よりFDSは無適用でハニング窓関数を適用した場合のPSDの図を作成したいと仮定します。最初に行わなければならない作業は作図を行うソフトウェアにPD001Aの結果ファイルを読込ませる作業です。エクセルをご使用になる場合は、WindowsのエクスプローラやMacのファインダの画面で目的とする結果ファイルをダブルクリックして頂ければ、通常はエクセルが起動して自動的に読込まれます。ただし、ファイルの拡張子"csv"をエクセル以外に関連づけされている場合はまずエクセルを起動してから目的の結果ファイルを開いて頂くことになります。エクセル以外のソフトウェアをご使用になる場合はあらかじめお好みのテキストエディタで結果ファイルを読込み、最初の行(ヘッダ行)を削除したファイルを別途作成したほうが便利かもしれません。ただし、当事業所ではお客様の結果ファイルの保存は行いませんので、結果ファイルの内容を変更される場合は事前にコピーを作成してお客様ご自身で保存されることをお勧めいたします。
次に作図する範囲を周波数または周期で決め、その範囲がどの行からどの行になるかを結果ファイルの第1列(周波数)または第2列(周期)を参照して探します。エクセルではA列またはB列になります。次にこの例での作図対象はFDSは無適用でハニング窓関数を適用した場合のPSDですが、それがどの列にあたるのかを表2Aを用いて探します。この作図対象はケースC1のPSDに相当し、表2Aより30列目(エクセルではAD)になることがわかります。後はこの30列目で作図したい範囲の行を選択し、エクセルその他のソフトウェアで作図するだけです。
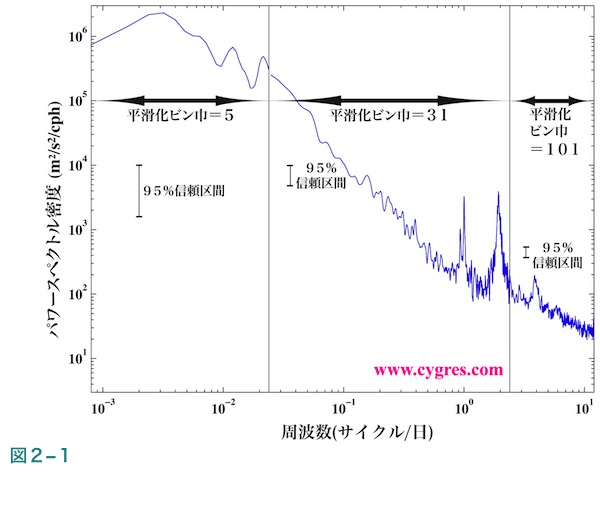
なお、作図上の注意事項ですが、(2-2)に記述するようにPSDの図を作成する場合は一般的には縦軸に対数スケールを用います。これは通常はPSDの変化の幅が非常に大きく、一般的によく使う均等(線形)スケールで作図すると非常に大きな値以外は見えなくなってしまうためです。また、図1-1(b)に示すように比較的広い周波数幅のPSDの作図を行うと高周波域でのPSDの大きな変動が目立ち過ぎる場合があります。このような場合は低い周波数域ではケースA1、B1またはC1の結果を用い、中間の周波数域ではケースA2、B2またはC2の結果を用い、高い周波数域ではケースA3、B3またはC3の結果を用いて作図すると見やすい図ができる場合があります。図2-1はこのような方法を用いて作成した図で、図中の黒の縦線はケースを切り替えた境界を示します。図2-1中の信頼区間については次の(2-1-3-2)に記述致します。この図のPSDの計算に用いたデータは図1-1(b)の計算に用いたデータと同じですが、図1-1(b)では全周波数域においてFDSビン巾7のFDSを適用した結果となっています。なお、図2-1のような図を作成したい場合はあらかじめ結果ファイルよりそれぞれのケースから作図に使用したい範囲の値だけをコピーして別のワークシート等にペーストして作図したい値だけを含むような新しいワークシート等を作成したほうが便利です。
(2-1-3-2) PSD及びPSDの信頼区間の使用方法
PD001Aでは9ケースの計算結果をご提供致しますが、これらのうちどれか1つのみを採用し、他はすべて無視しなければならないという理由はありません。例えば全周波数域の大雑把な様子を見たい場合はケースA3、B3またはC3の結果を使用すると便利と思われます。ハニング窓関数はPSDを計算する際に比較的広く用いられている、いわば汎用の窓関数で、お客様がPSDを他の方に見せる必要がある場合などは窓関数についての説明はただ単に広く使われているということだけで済ませられますので、ケースC3の結果を用いるのが便利と思われますが、(4-2-3)で記述するようにハニング窓関数の適用が適切でない場合もあります。もしFDSのビン巾があまり違わないにもかからわず、ケースA3とケースC3のPSDに大きな差がある場合はお客様のデータについてはハニング窓関数の適用があまり適切ではないことも考えられます。より細かくPSDを見たい場合はその細かさによりケースA2、B2またはC2のどれか、あるいはケースA1、B1またはC1のどれかをご使用されればよいと思われます。ただし、ケースA1の結果を使用される場合は後で記述するように若干の注意が必要となります。
特定の変動の周波数を出来るだけ正確に知りたい場合はFDSを適用しないため周波数解像度が高いケースA1またはB1のどちらかを使用されればよいかと思われます。一般的にはケースA1やB1の結果には非常に沢山のピーク(変動が大きい周波数)が現れますので、目的のピークを確定するためにはケースA2やB2の結果も参照されたほうがよいかもしれません。ケースB1の解像度はテューキー窓関数のテーパー比で変わりますが、デフォルト設定の場合はケースA1の解像度とほとんど同じで、ケースC1は(4-2-6)で記述するようにハニング窓関数が持つFDSに似た効果により周波数解像度がケースA1及びB1に比べやや低下します。なお、FDSを適用した場合のPSD(デフォルト設定の場合はケースA1、B1及びC1を除く全ケース)は(4-3-1)で記述するように値が小さくなりますのでご注意が必要です。
ここでケースA1についてですが、統計の専門家は一般的にはケースA1の結果は使用しません。その理由を簡単にご説明いたしますと、まず、統計の専門家は通常はお客様が実際にお持ちのデータは統計的性格が同じような無数のデータセットの中の単なる1つのデータセットと見なし、お客様のデータを用いてPD001シリーズで計算したPSDはその無数のデータセットによってあらわされる真のPSDの単なる推定の1つにしか過ぎないと考えます。そうすると、計算されたPSDは推定された値にしかすぎないのですから、真のPSDに何らかの誤差が加わった値であると考えられます。なお、この誤差というのは補足1に記述するような数値計算を行うと常に生じる計算上の誤差とは無関係です。
ここで、真のPSDは通常は手持ちのデータから計算できるものではなく、場合によれば仮想的なものです。統計の専門家はできるだけ精確に真のPSDを知ることを望むわけですが、統計の理論を導入するとケースA1の結果に含まれていると推定される誤差は非常に大きく、従ってケースA1の結果は使用できないという結論に至ります。ケースB1の結果についてもテーパー比がデフォルトの値であれば、統計の専門家は多分使用しないでしょう。他のケースの結果については、統計の理論によれば誤差を減少させる効果がFDSにあるので使用しても差し支えがないと考えられます。ここでこの誤差の大きさですが、これは計算されたPSDの確かさの範囲という形でPSDの信頼区間によって示されます。なお、こういった議論や実際のPSDの信頼区間の計算は基本的にはデータの単純な平均によって得られるサンプル平均値(推定された平均値)とデータが属する母集団とよばれるものの平均(真の平均値)との関係と似ていて->ここ<-にもうすこし詳しく記述しています。(実際は母集団の平均ではなく分散の推定と同じです)
ここで、もしお客様が実際には計算できない言わば仮想的な真のPSDにはまるで興味がなく、お持ちのデータのPSDが知りたいという場合は上のような統計の専門家の議論は無意味と言えるかもしれません。したがってそのような場合はケースA1の結果を使用してもかまわないと思われますが、その際にはPSDの信頼区間は意味をもちません。これはPD001シリーズで計算するPSDの信頼区間は上に記述したような統計の専門家の考えを基礎にしているからです。また、(2-1-3-3)で使用しているようなデータについては、そもそもデータの値に統計的にしか記述できない要素がまったく無く、また、データ長やデータの開始時間も決められているため上に記述したような誤差がデータには一切含まれていません。したがってこのような場合についてもケースA1の結果を使うことにはまるで問題がありません。なお、このような場合はPD001シリーズで計算するようなPSDの信頼区間は無意味なものとなります。これに対し(2-1-3-5)で使用しているようなデータの場合は、本来は統計的にしか記述できない要素である式(7)中のノイズが含まれているため、ケースA1の結果を使用される場合は上に記述したような点について留意されたほうがよいと思われます。また、(2-1-3-3)で使用しているようなデータについてもデータの開始時間やデータ長が不規則に変わるような場合は統計的にしか記述できない要素が加わります。
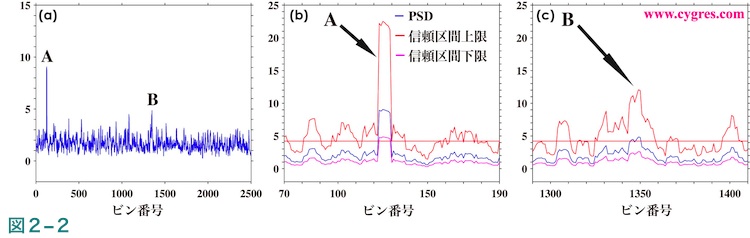
PSDの信頼区間の使用方法については具体例を用いて説明致します。図2-2(a)は細かいピークが非常に多いが全体としては比較的平坦なPSDの例を示します。この図中のAは最大のピークでBは2番目に大きなピークです。ここで問題となるのはこれらのピークがはたして特別なのか、それとも他の無数のピークと同様のものなのかという点ですが、それを判断するためには通常はAやBのピークが他と比べて特別に高いかどうかを調べます。そこで、最初に行う事は比較の基準となる”普通の高さ”を決めることになりますが、ここで、”普通の高さ”の値を”底”と呼ぶ事にします。この”底”の決め方はいろいろあるのですが、ここでは全周波数域でのPSDの95%の信頼区間の上限の平均値を”底”とします。なお、他の”底”の決め方としてはPSDそのものの平均、あるいはPSDそのものの平均にPSDの標準偏差の3倍を加えたもの等が考えられます。またPSDが図2-2(a)のように平坦ではなく傾斜が明確に見える場合等は大雑把に傾斜を求めてそれを”底”にする、あるいは調べたいピーク周辺にのみ平均を計算する周波数域を限定する等も考えられます。その他、周波数による特定の分布を仮定し、実際のPSDの計算結果を用いて調整したものを”底”にするといったことも行われます。いずれの方法を採用するにしろ、”底”を決める場合はその方法が妥当であることが大事ですが、そのためには最初に図2-2(a)のような図を一度眺めてみる必要があります。
さて、ここで図2-2(b)にPSD(青線)、PSDの95%の信頼区間の上限(赤線)、PSDの95%の信頼区間の下限(紫線)及び”底”(水平の赤線)をA周辺のみ拡大して示します。この図によれば、Aの信頼区間の下限(紫線)は”底”(水平の赤線)より上にありますが、このような場合は95%の信頼限界でAは”普通”に比べて大きい、すなわち特別と見なせます。これに対し図2-2(c)はB周辺を拡大表示したものですが、こちらの場合はPSD(青線)及びその信頼区間の上限(赤線)は”底”より高いのですが、信頼区間の下限は”底”より低くなっています。このような場合は95%の信頼限界でBは特別とは見なせないということになります。図2-2(a)によれば他の無数のピークはすべてBより低いのですから、このデータではAのみ特別で他はすべて普通となります。
上の例ではPSDは比較的平坦でしたので縦軸に均等スケールを採用しましたが、実際にはPSDの変動巾が大きいため縦軸を対数スケールにしたほうがよい場合がしばしばあります。縦軸を対数スケールにすると図中での見た目のPSDの信頼区間の上限と下限の巾はFDSの巾を一定に保つ限りどこでも同じになります。したがって、図1-1(b)の場合では信頼区間は図中の一カ所にだけ表示すればよく、図2-2のように全周波数域に折れ線で表示する必要はありません。図2-1の場合は周波数域によって異なるFDSの結果を使用しているため、計3カ所に信頼区間の巾を表示しています。
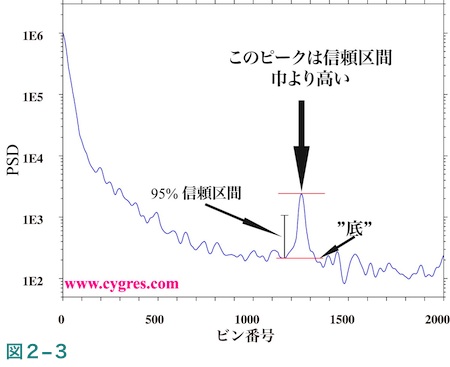
さて、ここで図2-3にこのような場合の信頼区間の使用例を示します。この例ではPSDは対数スケールを採用しても変動が大きく、全周波数域で”底”を決めるには曲線を採用しなければいけませんが、ここでは短い赤の水平の線で囲まれたピークを調べるためにかなり大雑把にその麓にあたる周辺の値を”底”としています。この図の例ではこの赤の水平線で囲まれたピークの高さは信頼区間の巾より高いので、特別と見なせますが、他のピークはそれぞれの麓を”底”にするとどれも高さが信頼区間の巾より低いので特別とは見なせません。
なお、信頼区間による判断は色々な仮定に基づいた一般的な統計理論の適用にすぎず、データの変動を実際に生じさせている物理的その他の過程は一切考慮されていません。従って、信頼区間を用いて特別と判断されたピークでもそれが実際に意味のあるものという保証はできませんし、また、信頼区間を用いて普通と判断されたピークが実際に意味のないノイズのようなものという断定もできません。以上により、信頼区間のみでPSDの図上にあらわれたピークの重要性を判断するのはあまりお勧めできません。PSDの信頼区間はPSDの図上に現れた無数のピークの中から特定のピークを選んだ場合において、その特定のピークを選んだ事を正当化するために使用する程度に止めておいたほうが無難ではないかと思われます。