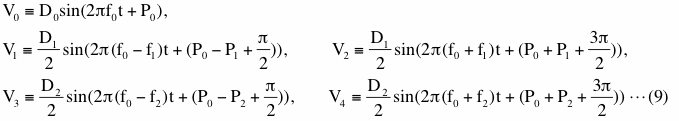お問合せは
->こちらへ<-

パワースペクトル密度計算 (スペクトル解析)
小額定型計算 PD001A/B
小額定型計算業務はお取り扱いするデータの形式、計算内容、計算結果の内容及び形式やデータ授受方法といった業務全般を定型化することでコスト削減及び納期短縮を図った計算サービスです。科学、技術研究のみではなく、商業や工業のいろいろな分野のデータの解析にご利用下さい。小額定型計算業務については->こちら<-をクリック下さい。
図を含む本文書の著作権はCygnus Research Internationalに帰属します。無断転載はお断り致します。
PD001A/B ユーザーガイド 3/7
目次
(1章) PD001シリーズの要約
(1-1) PD001シリーズで行う計算について
(1-2) お客様がご指定できる計算設定項目の要約
(1-2-1) トレンド除去; 全てのケースで個別に指定
(1-2-2) PSDの値の信頼区間のパーセンテージ; 全ケースで同一の値を指定
(1-2-3) テューキー窓関数のテーパー比; ケースB1、B2及びB3のみ適用 値は個別に指定
(1-2-4) 周波数領域での平滑化(以下FDSと略)ビン巾; ケースA1、B1及びC1の3ケースを除く全ケースで個別に指定
(1-3) 計算手法
(1-4) 入力データ(お客様のデータ)について
(1-5) プロダクツ
(1-5-1) 結果ファイル
(1-5-2) PDF形式の図
(1-6) 料金、納期およびご発注手順
(1-7) 個人情報、お客様のデータに関する情報保護
(2章) プロダクツの詳細及びその使用例
(2-1) 結果ファイル
(2-1-1) 結果ファイルのフォーマット(形式)
(2-1-2) 結果ファイルに記述する計算結果の内容
(2-1-2-1) 周波数 (Frequency)
(2-1-2-2) 周期 (Period)
(2-1-2-3) PSD (PSD)
(2-1-2-4) PSDの信頼区間 (Conf Int)
(2-1-2-5) 分散のパーセンテージ (% of Var)
(2-1-2-6) 振幅 (Amplitude)
(2-1-2-7) 位相 (Phase)
(2-1-3) 結果ファイルに書き出された情報の利用方法及び使用例
(2-1-3-1) 結果ファイルの値を用いて独自の図を作成したい場合
(2-1-3-2) PSD及びPSDの信頼区間の使用方法
(2-1-3-3) 特定の周波数での変動の巾(大きさ)を知りたい場合
(ケース1) 信号は振幅が一定の単一の周波数の三角関数で表される場合
(ケース2) 信号は振幅が一定の異なった周波数の三角関数を足し合わせたもので表される場合
(ケース3) 信号は単一の周波数の三角関数だが、振幅が時間とともに変動する場合
(ケース3-1) 信号の振幅の変動そのものが三角関数の形の場合
(例1) 信号は三角関数で周波数はf0。信号の振幅は周波数f1の三角関数の形で変動
(例2) 信号は三角関数で周波数はf0。信号の振幅は定数に周波数f1の三角関数を足し合わせた形で変動
(ケース3-2) 信号の振幅の変動そのものは三角関数ではない場合
(ケース4) 信号は周期的だが、三角関数の形ではない場合
(2-1-3-4) 特定の周波数域内の変動が全体の変動と比べてどの程度強いのかを知りたい場合
(2-1-3-5) 簡易デジタルフィルター(PD001Aのみ適用)
(2-1-3-6)データ中の値の変動の振幅を求める他の方法
(2-2)図
(3章) PD001シリーズ用のデータファイルの作成手順例
(4章) 各種指定項目の設定について
(4-1) トレンド除去;有無 無指定時は有
(4-1-1) トレンドとは? 除去の目的は?
(4-1-2) トレンド除去の例
(4-1-3) トレンド除去で問題が発生する例
(4-2) テューキー窓関数のテーパー比;%で表したテーパー比 無指定時は10%
(4-2-1) 窓関数を適用する理由
(4-2-2) 窓関数の適用とは
(4-2-3) ハニング窓関数;使用すると問題が生じる場合について
(4-2-4) 本小額定型計算業務 PD001Aでハニング窓関数を適用したPSDのみではなく、窓関数非適用及びテューキー窓関数を適用したPSDも計算する理由
(4-2-5) ハニング窓関数によるデータ両端近くの減衰を少なくする方法
(4-2-6) 窓関数が持つFDSに似た効果について
(4-2-7) IFDSは必ずしもPSDを平滑化しない
(4-2-8) 窓関数適用によるPSDや振幅スペクトル減衰に対する補正
(4-2-9) 窓関数適用時の補正の効果
(4-2-10) テューキー窓関数のテーパー比がPSDに与える影響
(4-3) 周波数領域での平滑化(FDS)ビン巾; 1、3、5、7等奇数 無指定時は無し(1)、3及び7
(4-3-1) PSDに対するFDS
(4-3-2) 振幅スペクトルに対するFDS
(4-3-3) FDSを適用した場合の周波数解像度
(4-3-4) FDSに代わる他の平滑化法
補足1 コンピュータを用いて計算をする際に生じる誤差について
補足2 パワースペクトル密度関数のスペクトル漏れと窓関数の関係について
補足3 データ長が短いと単一のピークが現れ、長いとツインピークが現れる理由
補足4 S1のトレンド除去により付加される直線成分のPSDの悪影響に対するS1とSRの周波数の関係
(2-1-3-4) 特定の周波数域内の変動が全体の変動と比べてどの程度強いのかを知りたい場合
(2-1-2-5)に記述したように分散はデータの値の変動の大きさを表すので、このような場合は結果ファイルに書き込まれた分散のパーセンテージを使用します。具体的にはある周波数f1とf2の間の周波数域に含まれる変動が全体の変動と比べてどの程度なのかを知りたいのであれば、結果ファイルの1列目でf1とf2に該当する行を探し、次にその間の分散のパーセンテージ、目的とするケースに従い6、12、16、20、25、29、33、38または42列目(表2A)、を足し合わせればよいということになります。
(2-1-3-5) 簡易デジタルフィルター(PD001Aのみ適用)
結果ファイルに書き込まれたケースA1の振幅(式(3)のAmに相当)及び位相(同Smに相当)のうち特定の周波数域の値のみを取り出し、他の周波数域の値はゼロにして式(3)に代入して計算することにより、元データの特定の周波数成分のみを取り出すという簡単なフィルター操作を行うことができます。図2-18(a)はこのようにして高い周波数域のみを通過させるフィルタ(以下HPFと略)、特定の周波数域のみを通過させるフィルタ(以下BPFと略)及び低い周波数域のみを通過させるフィルタ(以下LPFと略)を図1-1(a)に示したデータに適用した結果得られる時系列データを示します。なお、このデータの変動の最短周期はサンプリング間隔より2時間=1/12日になりますので、HPFの通過周波数上限は12サイクル/日となり、最長周期はデータ長より1250日になりますので、LPFの通過周波数下限は1/1250サイクル/日となります。なお、この図では違いを見やすくするために各フィルタ適用結果は0の位置を少しずつ縦にずらして描画しています。また、一番下の赤線はフィルタ適用前のデータで図1-1(a)と同一です。これらの図によりLPFを適用した結果は元データの全体的な変動をよく再現していることがわかります。
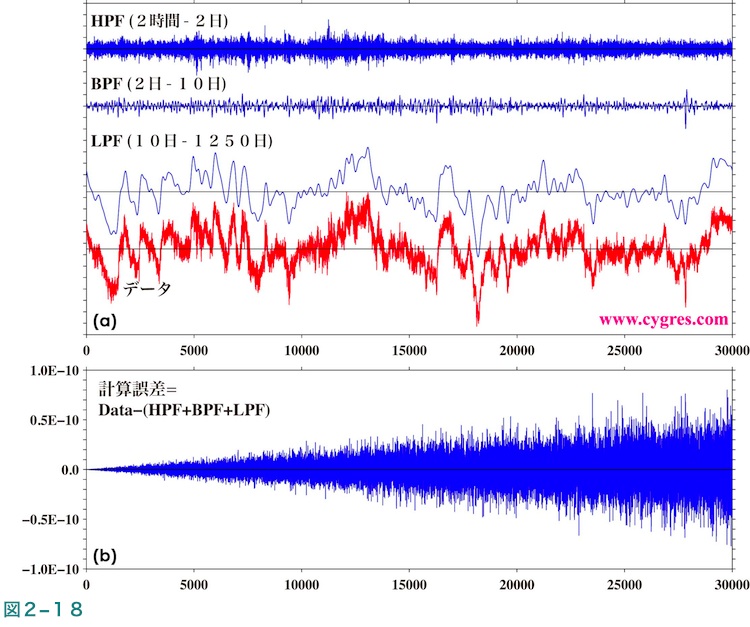
ここで、HPF、BPF及びLPFの各フィルタの通過周波数域を足し合わせると元データの全周波数域を含むことになるので、図2-18(a)に示したフィルタ適用後の時系列を全部足し合わせると基本的には元データが再現されることになります。図2-18(b)に示すのはそのようにして再現した元データと実際の元データの差の時系列ですが、これは前述した数値計算上の計算誤差になります。元データの最大値は100.0を越え、また標準偏差は約31.9ですので、それに比べれば図2-18(b)に示す計算誤差は通常の用途では無視できるほど十分に小さいことがわかります。
このようなフィルタ操作の応用として、ノイズを含んだデータから信号を抽出する操作が考えられます。ここでは最初に比較的ノイズの強度が弱い場合の例を示します。ここで使用するテストデータは(2-1-3-3)のケース3-2に類似したもので、下のようになります。
![]()
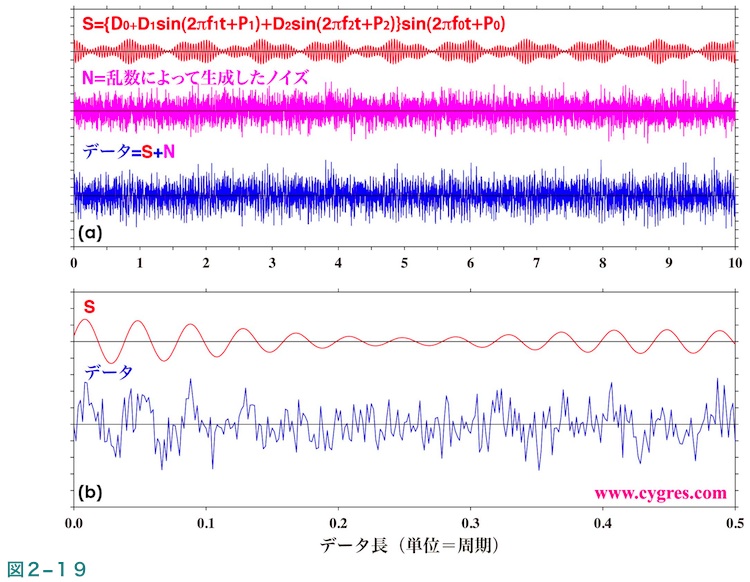
この式中でD0、D1、D2、f0、f1、f2、P0、P1及びP2はすべて定数です。このデータは信号としては下の式(8)のように5つの周波数の信号が含まれています。
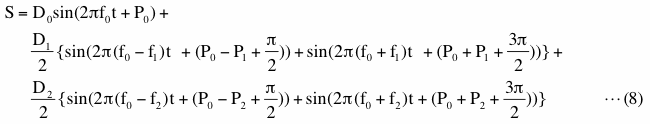
図2-19(a)にここで使用する信号(S)、ノイズ(N)、及びデータ(S+N)の時系列を示しますが、式(8)中の各定数はD0=0.8、D1=0.4、 D2=0.3、 f0=100、 f1=4、f2=10、P0=0.25、P1=2.35及びP2=1.14としています。なお、各時系列は0の位置を少しずつ縦にずらしていて、これまでの例と同様に縦軸の単位は省略しています。ノイズは標準偏差が1.0になるような乱数で代用していますが、これにより図2-19(a)で示されるようにノイズの強さは信号の振幅と概ね同程度となっています。なお、図2-19(a)の水平軸の単位は1/f1(下の式(10)のV1の周期)です。図2-19(b)は信号S及びデータの最初の部分を拡大した図で、両者の山(または谷)の位置を比較すると、データに信号が含まれていることがわかります。
ここで信号に関してV0、V1、V2、V3及びV4を以下のように定義します。
この定義により式(7)は以下のように簡潔に表現できます。
![]()
ここで、V0の周波数を含むビンを信号ビン0、V1の周波数を含むビンを信号ビン1のように定義します。図2-20(a)及び(b)は信号ビン1及び2の振幅及び位相がデータが増えるにつれどのように変化するかを示します。これらの図の水平軸の単位(図2-20(d)の下に表記)はV1の周期で、最初の1周期分は結果の変動が大きいので省略しています。V1およびV2の実際の振幅は同じ(=D1/2)で図2-20(a)中には黒の水平の実線で示しています。実際の位相についてはV1とV2では値が異なりますので、図2-20(b)中にはそれぞれ青色と赤色の水平の実線で示しています。図2-20(c)及び(d)は信号ビン3及び4の図である以外は(a)及び(b)と同じです。これらの図の詳細はかなり見にくいのですが、図の右端近くでは計算結果が比較的安定した同一パターンの繰り返しになっていることがわかります。図2-20(a)及び(c)中の青色の縦の実線で示したデータ長A、B及びCでの振幅スペクトル等は後で示します。なお、V0についてはここでは省略しています。
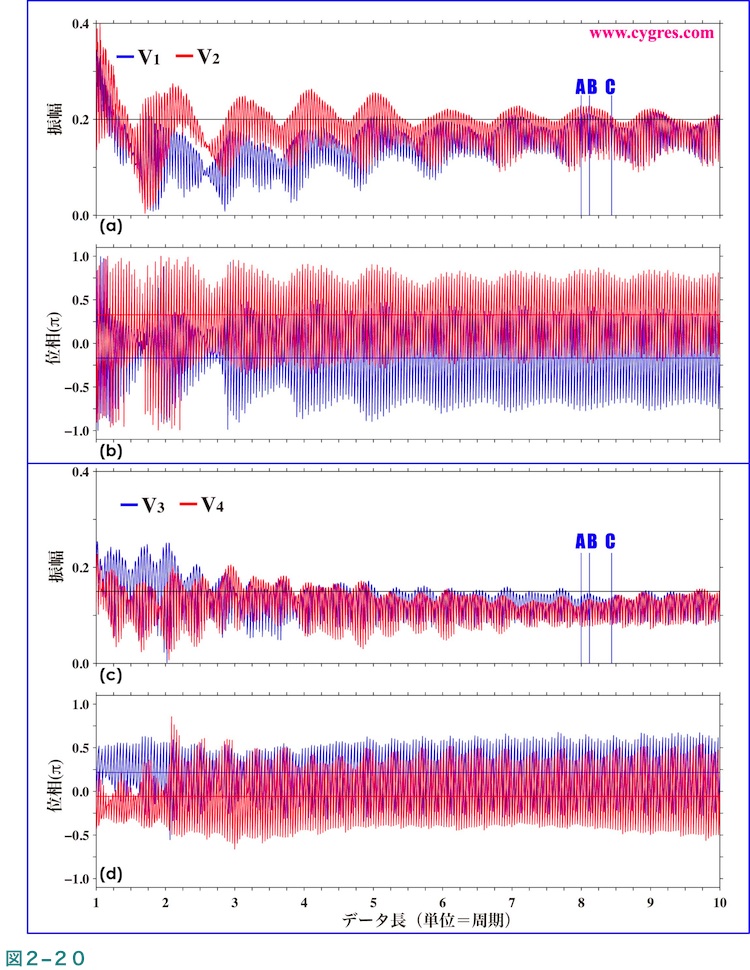
図2-21はデータ長7.9から8.5迄の間のみ取り出し水平方向に拡大した信号ビンの振幅及び位相の図で、図中の垂直や水平の実線の意味は図2-20と同じです。データ長がAの場合はすべての信号ビンについて周波数一致が成立していますが、図2-13で示した結果と異なり、ノイズのため信号ビンの振幅は実際の信号の振幅に一致していません(図2-21(a)及び(c))。なお、データ長Bはすべての信号ビンについて周波数一致が成立していない場合で、データ長Cは信号ビン3及び4の周波数はかなり実際の信号の周波数に近い場合です。
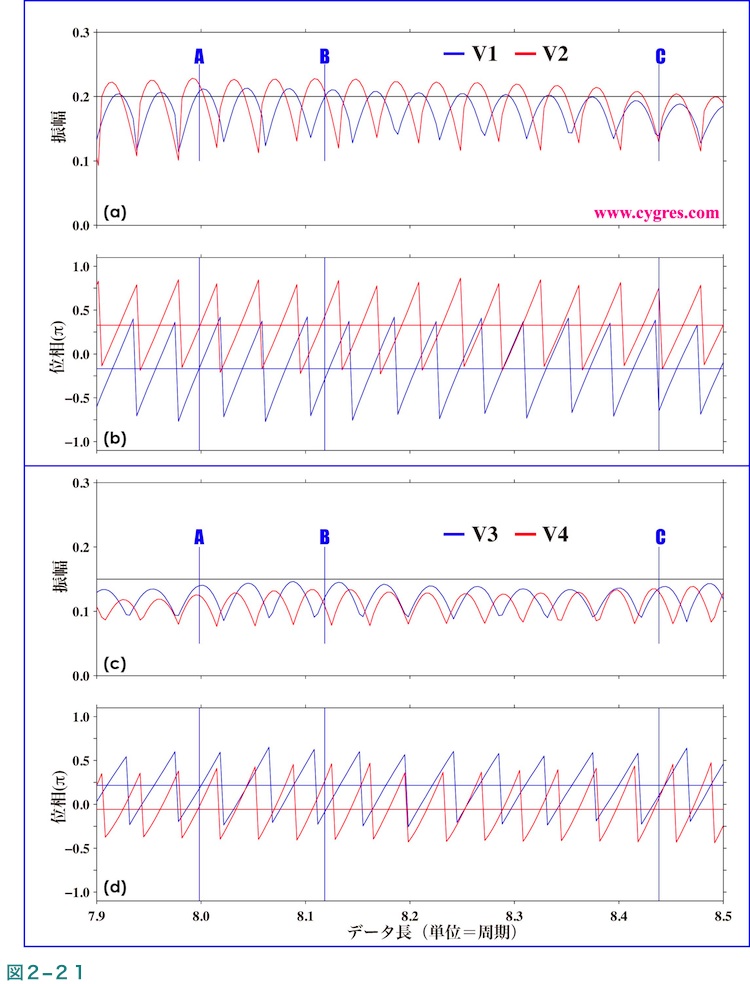
図2-22にデータ長がA、B及びCの場合の窓関数非適用の振幅スペクトルを示します。なお図の青線は式(7)や(10)のようにノイズを含むデータより計算した結果で、赤線は式(8)のようにノイズを含まない信号だけのデータから計算した結果です。この図の青線のスペクトルよりここで使用したノイズそのもののスペクトルは全周波数領域で比較的平坦なものであることがわかります。なお、描画の際には先に青線を描いてから赤線を描いているため、青線と赤線の位置が一致するような所では青線の上に赤線が上書きされています。
データ長がAの場合は周波数一致が成立していますので、ノイズを含まないデータ(赤線)については(4-2-1)で記述するように信号のスペクトル漏れがないケースで、図2-22(a)でも図2-5(a)と同様に信号のある周波数以外では振幅は実質ゼロになっています。ただし一般的には異なった周波数の複数の信号が存在する場合はこのケースのようにすべての信号について周波数一致を成立させるのは困難です。ここで示す例の場合はすべての信号について周波数一致が成立できるような周波数を意図的に選択していますのでご注意ください。データ長がAでない場合(図2-22(b)及び(c))は周波数一致が成立しませんので前述のように信号のスペクトル漏れが発生し、結果として全周波数領域で振幅の値がゼロより大きくなります。ただし、ノイズのあるデータ(青線)の場合はノイズの振幅のほうがスペクトル漏れの影響よりかなり大きいためスペクトル漏れの影響は視認できません。
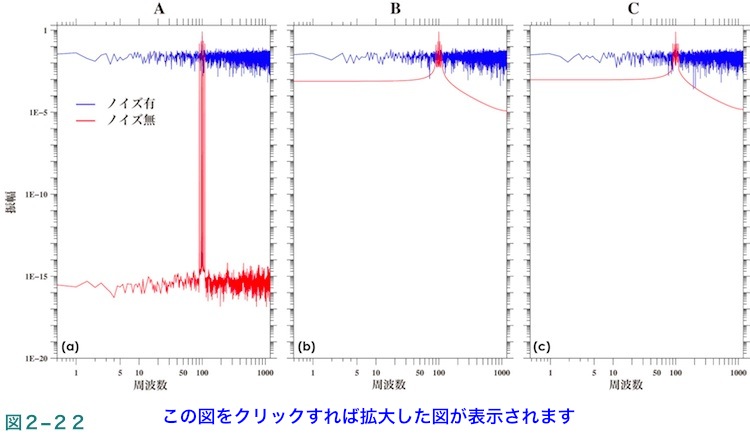
図2-23はノイズを含まない信号のみの場合(図2-22中の赤線)について信号のある周波数付近を拡大した振幅スペクトルの図です。なお、値を読み取りやすくするためにこの図では縦横両軸に均等スケールを採用しビンのある位置をプラス記号(+)で示しています。図中の短い黒の水平の実線(各図につき5本)の中央の水平位置は実際の信号の周波数を、高さは実際の信号の振幅を示しています。データ長がAの場合(図2-23(a))は各信号ビンの振幅は実際の信号の振幅とほぼ同じで、どの信号のピークも単一の点を頂上に持つ鋭いピークになっています。これに対し、データ長がAでない場合(図2-23(b)及び(c))は信号ビンの振幅は実際の信号の振幅より小さく、また信号のピークも巾の広いものになります。
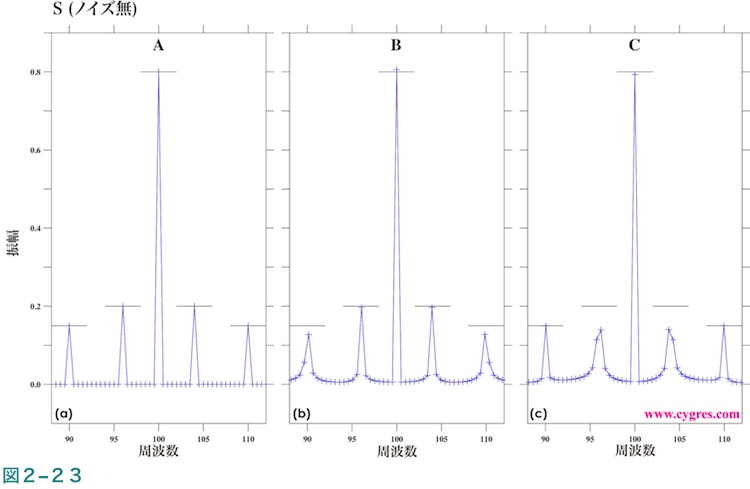
図2-24はノイズを含むデータの振幅スペクトル(図2-22中の青線)の図であること以外は図2-23と同じです。ここで使用したデータのノイズの大きさは図2-19で示したように時系列図ではデータ中の信号を見いだすことを困難にしてしまう程ですが、この図で示すようにスペクトル図では容易に信号を見つけることができます。図2-24と図2-23を比較することにより、ここで使用した程度のノイズの大きさでは信号ビンの振幅にはあまり大きな影響が出ないことがわかります。
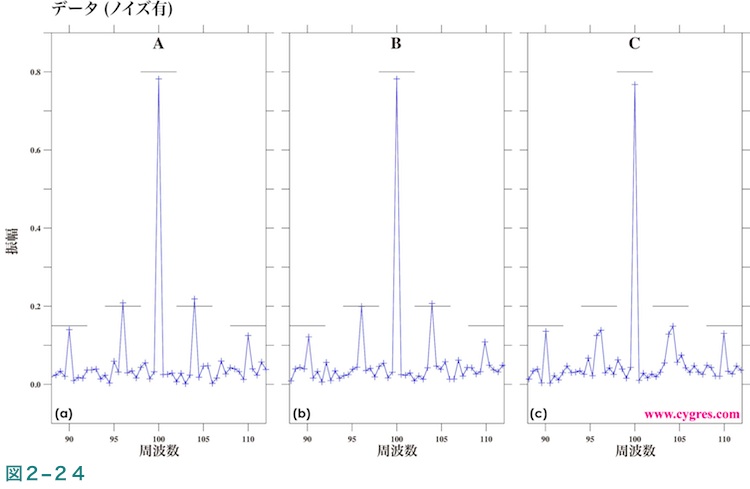
振幅スペクトルの値を用いてノイズを含んだデータから信号を再現する方法は幾つか考えられますが、ここでは2つの方法の結果を示します。まず、最初の方法は信号ビンの振幅及び位相の値のみを取り出し式(3)に代入する方法で、以下では方法1と呼びます。この方法を用いると、周波数一致が成立せず信号のスペクトル漏れが生じている場合は再現された信号が実際の信号より一般に小さくなり、変動の”山”や”谷”といった部分のずれも大きくなります。もう一つの方法は各信号について信号ビン及びそれらに隣接する高低両側のビン、計3ビンずつ取り出しそれらの振幅と位相の値を式(3)に代入する方法で、以下ではこれを方法2と呼びます。
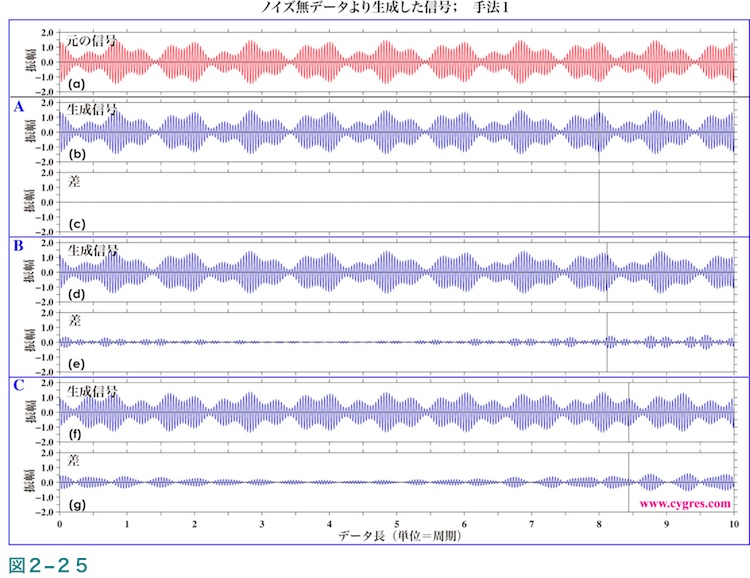
図2-25の最上段は実際の信号(式(8)及び図2-19(a)のS;ノイズは含まない)で、その下にデータ長A、B及びCについてノイズを含まない信号のみのデータの振幅スペクトルの結果(図2-22赤線、図2-23)を用いて方法1により再現した信号(以下では再現した信号をS'と略します)及び、それと実際の信号(最上段の図)との差を示します。なお、図2-25(b)〜(g)中の縦の黒の実線は振幅スペクトルを計算したデータ長を示します。
データ長Aで計算した振幅スペクトルを使用した場合はSとS'の差はほとんどないため図2-25(c)では値がゼロの所に水平の線が見えるだけです。これに対しデータ長B及びCで計算した振幅スペクトルを使用した場合はSとS'の差は図2-25(e)及び(g)で十分視認できるほどの大きさになります。SとS'の差は各図の縦の黒の実線(振幅スペクトルを計算したデータ長です)より左の部分の中央(図全体の中央ではありません)で最小となりその左右で対称となっています。ここで大事な点は、たとえノイズを一切含まない信号のみのデータより計算した振幅スペクトルを用いても、周波数一致が成立しない場合はこの方法では再現した信号と実際の信号との間にはそれなりの差が生じるという点です。
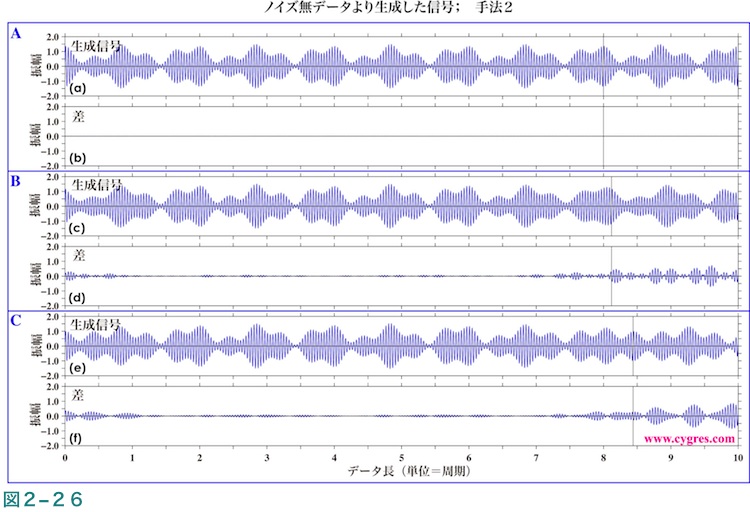
図2-26は方法2で計算したS'及びSとS'の差で図2-25(b)〜(g)に相当します。図2-26(d)と図2-25(e)、図2-26(f)と図2-25(g)を比較することにより、SとS'の差は方法1に比べやや小さくなっていることがわかります。なお、ここで使用したデータはノイズを含んでいませんので、各信号について3ビンだけではなく、より多いビンの値を使用して計算すると最終的には元の信号がほぼ完全に再現できます。
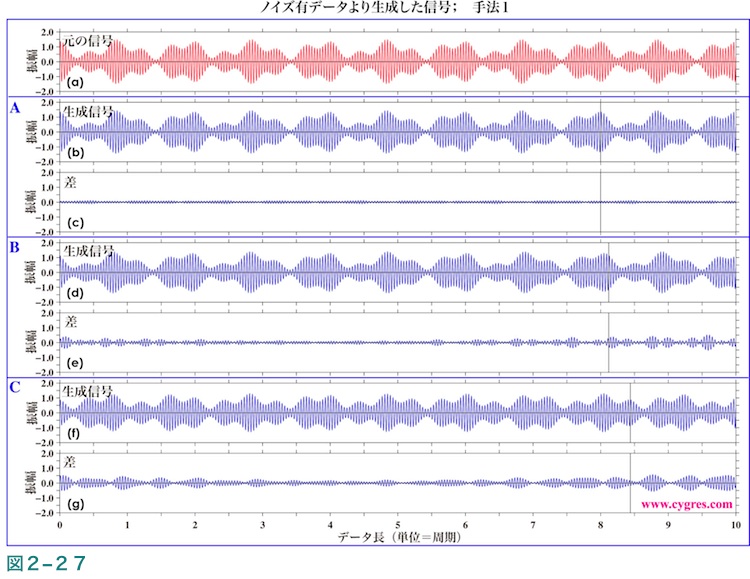
図2-27はノイズを含んだデータ(式(7)、(10)及び図2-19のデータ)の振幅スペクトルの結果を用いた以外は図2-25と同じ(方法1)です。この図よりSとS'の差は図2-25と比べ、やや大きくなっていることがわかります。
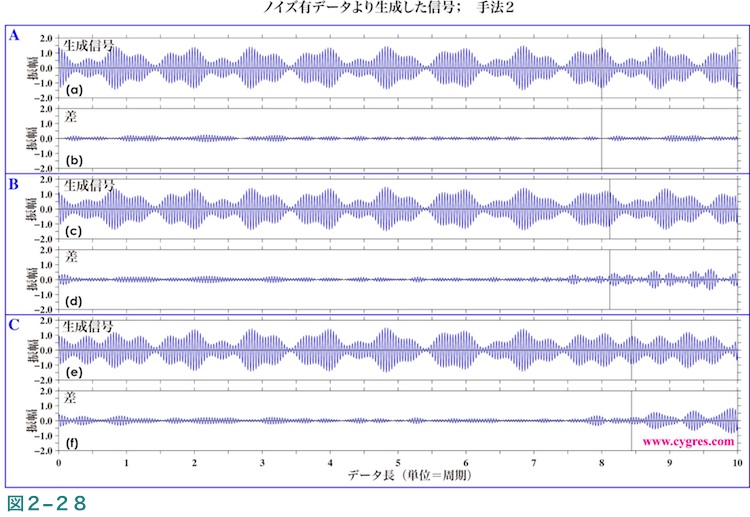
図2-28は方法2を用いてノイズを含んだデータの振幅スペクトルから計算した結果で、図2-26に対応します。この図より方法2を用いるとSとS'の差がやや小さくなることがわかります。ただしここではノイズを含んだデータを使用していますので、より多いビンの値を使用して信号を再現しようとすると、ノイズのないデータを使用した場合と異なりある時点でSとS'の差がノイズのためにかえって大きくなります。
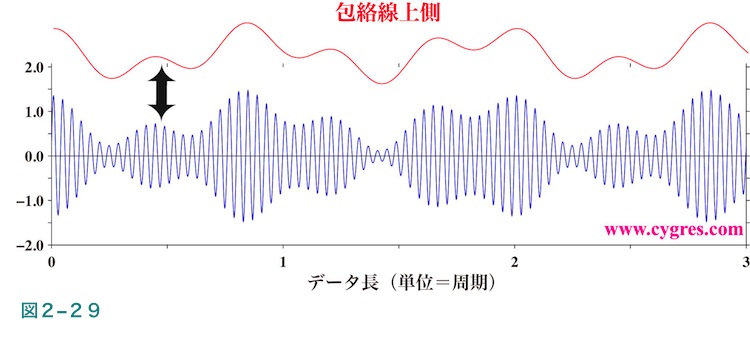
ここで実際の信号Sは式(8)で示すようにAM放送で言えば搬送波に相当する高い周波数f0の三角関数の振幅が音声などの信号により時間とともに変動しているとも見なせるのですが、場合によればSそのものよりは、安定した出力の信号を媒体を通して受信しその媒体の時間変動を調べる等、振幅の変動を知りたい事もあるでしょう。実際AM放送では情報は振幅の変動として送られるのであって、搬送波はただ単に情報を伝達するために必要な貨車やトラックのようなものでしかないと考えることができます。図2-29の青線に信号Sの一部を示しますが、この高い周波数の変動の振幅の変動のみを取り出したものが図の赤線に示す包絡線というものになります。この包絡線と呼ばれる赤線を下にずらすと青線の上側の輪郭に合致し、これがAM放送で言えば音声の波形になり、この波形は
![]()
で示されます。包絡線は下側にもあるのですが、この下側の包絡線は上側のものと対称なので省略します。
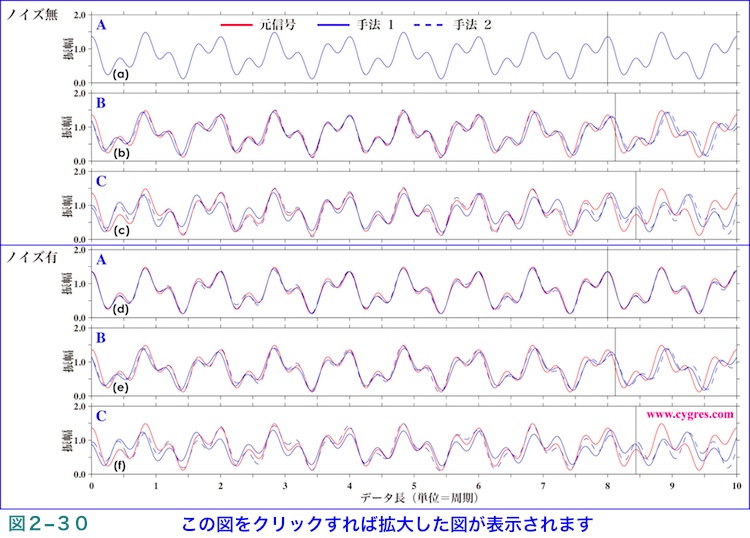
図2-30の上部3図は図2-25、2-26に対応し、S(赤色実線)、信号のみでノイズのないデータより方法1によって求めたS'(青色実線)及び方法2によって求めたS'(青色破線)の上側の包絡線を示します。図2-30の下部3図は図2-27、2-28に対応し、ノイズのあるデータより求めた結果です。図2-30(a)(最上段)では青の実線しか見えませんが、これはSとS'の値はほぼ同じなためです。図2-30より、(1)この程度の振幅のノイズを付加しても信号の再現精度にはあまり大きな影響を与えない、(2)信号の再現精度は各図の縦の黒の実線(振幅スペクトルを計算したデータ長です)より左の部分の中央(図全体の中央ではありません)で最も良いがそこから離れるにつれ悪化する、(3)実際の信号の周波数と信号ビンの周波数の不一致は信号の再現精度に悪影響を与えることがわかります。ここで(2)の理由は、周波数一致が成立しない場合は信号ビンの周波数(式(11)中のf1及びf2)が実際の信号の周波数と異なることになりますが、その場合にもしSとS'の包絡線が時系列図のある所(Xとします)で比較的よく一致しているとすると、Xから離れるに従いSとS'の差が周波数が合っていない為に大きくなりますが、ここではXが縦の黒の実線より左の部分の中央になるからです。ノイズの有無は(2)や(3)には関係してきません。
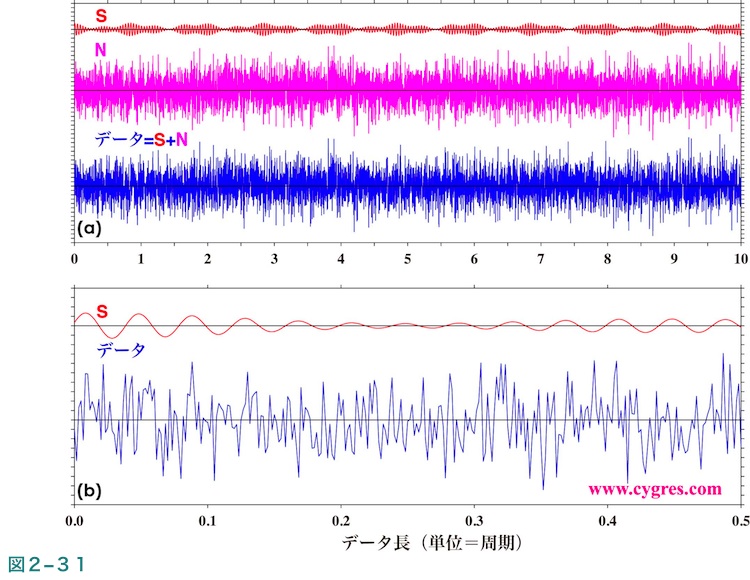
では、ここでノイズを3倍強くしてみます。図2-31にこの場合の信号(S)、ノイズ(N)、及びデータ(S+N)の時系列を示します。ここで、Sは図2-19(a)で示すSとまったく同じですが、前のSに比べ図2-31のSが小さく見えるのは図の縦方向のスケールを変えたからというだけの理由です。ここで使用するノイズの標準偏差は3.0で、図2-31(b)では前例(図2-19(b))と異なりデータ中に存在する信号を視認するのは困難です。
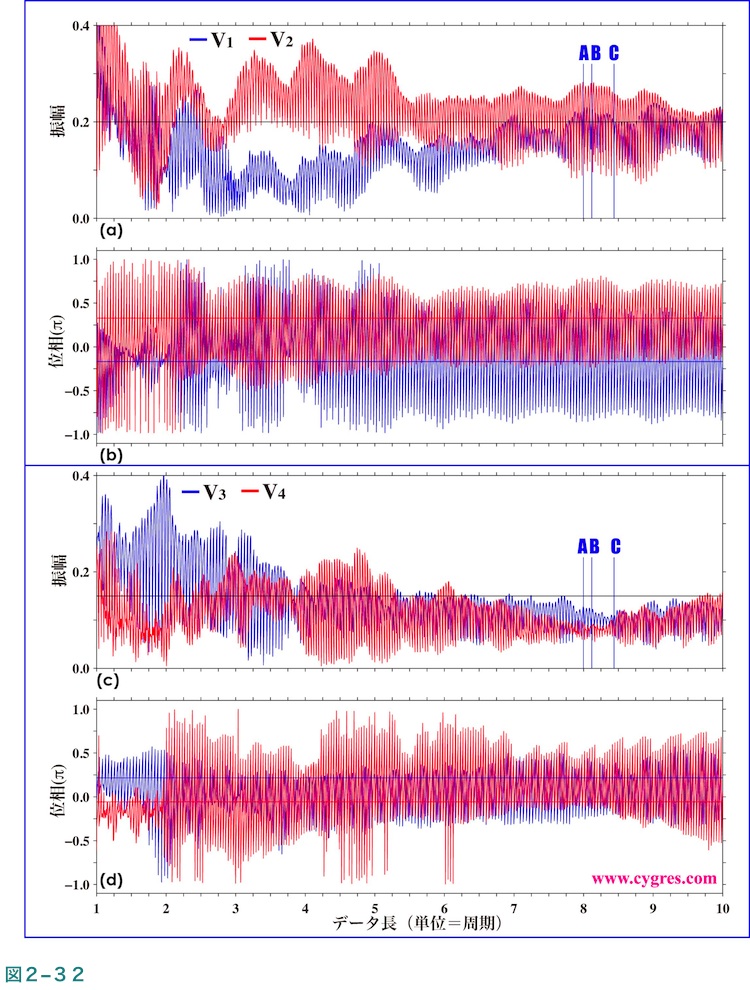
図2-32は各信号ビンの振幅及び位相がデータが増えるにつれどのように変化するかを示しますが、各信号ビンの振幅の変動は前例(図2-20)と比べかなり大きくなっています。この図よりこの例では精確な振幅を得るためには比較的長いデータ長が必要となることがわかります。以下で示す振幅スペクトル等は前例との比較のため図中の短い青の実線で示した前例と同じデータ長を使用しますが、この図から判断する限り、それらのデータ長は精確な振幅や位相を得るためにはやや短すぎるようです。
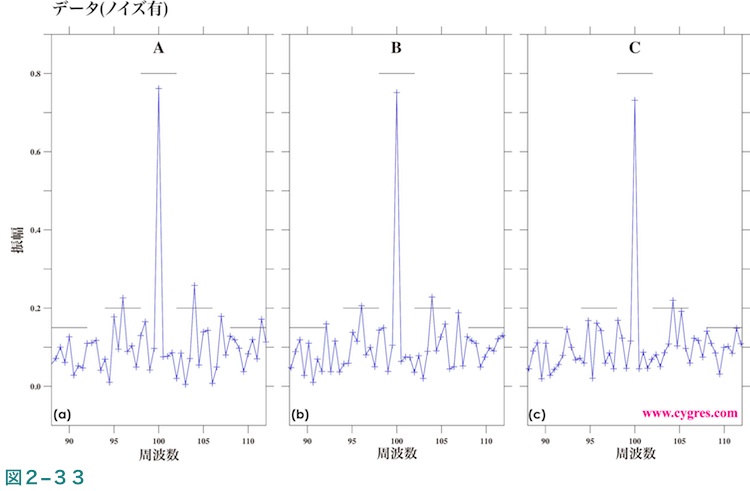
図2-33はノイズを含むデータについて信号のある周波数付近を拡大した振幅スペクトルで図2-24と同様の図です。この振幅スペクトルと図2-24の振幅スペクトルを比べると、この例ではノイズによるピークが信号のピークと同程度の高さになり、振幅の値だけではどれが信号でどれがノイズであるかを判定するのは困難なことがわかります。
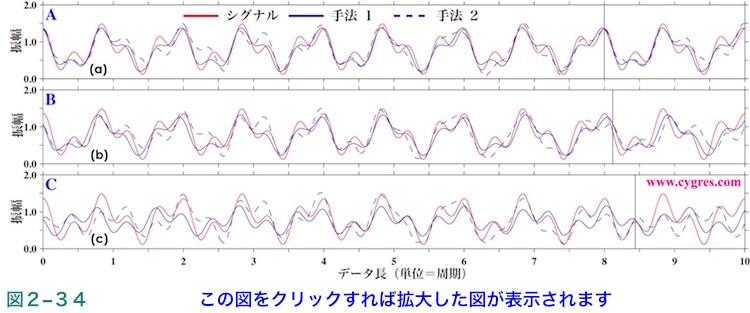
図2-34にSおよび前例と同様の方法で計算したS'の上側包絡線(前例は図2-30です)を示します。この図から判断する限り、この例ではノイズが信号に比べかなり大きいにもかからわず、信号は比較的よく再現されているように見えます。この例での最大の問題は信号の周波数が既知でない場合、図2-33のような振幅スペクトルのみではどれが信号ビンであるかを判断することは不可能に近いという点です。
(2-1-3-6)データ中の値の変動の振幅を求める他の方法
ここではスペクトルの計算を行わずにデータ中の変動の振幅を求める方法を記述します。この方法による計算を本小額定型計算業務 PD001シリーズに含める予定はありませんが、お客様のご要望が多数あれば別の小額定型計算業務として提供いたします。
ここでご紹介するのはデータの値は互いに相関のない一つ以上の信号及び信号と一切相関がない誤差が足し合わさったものと考え、与えられた信号の周波数に対しデータよりそれらの信号の振幅と位相を統計的手法で計算するという方法です。これを数式で表現すると以下のようになります。
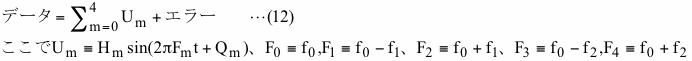
この式で与えられているのはデータ及び周波数Fmで、求めるのは振幅Hm及び位相Qmです。副産物として”エラー”も得られますが、通常はその値は使用しません。ここで重要なのは上の式中のUmと式(10)中のVmとの間には周波数が同じという以外にははっきりとした関係が無く、また、上の式中の”エラー”は式(10)中のノイズと一切関係が無いという点です。式(12)はデータと計算の結果(HmやQmは統計的な計算によって求められる値です)の関係を示す式で、これに対し式(10)はどのようにしてデータが構成されているかを示す式で、両者は根本的に異なる式です。式(10)中のノイズは乱数によって作成しましたので、このノイズとV0、V1、V2、V3及びV4との相関は小さく一般には相関が無いと言えるのですが、実際に相関係数を計算するとゼロではありません。それに対し、ここで記述する方法は式(12)中のU0、U1、U2、U3及びU4と”エラー”との相関係数がゼロになるようなHm及びQmを統計的手法で求めます。
なお、この方法を適用するためには事前に目的とする信号の周波数を正確に知っていなければなりませんが、スペクトルの計算と異なり、周波数一致に気を使う必要はありません。またデータのサンプリング間隔は一定でなくても構いません。以下に示す結果を見るとこの方法の方がスペクトルの計算より便利に見えるかもしれませんが、本来スペクトルを計算する一般的な理由は未知の信号の振幅だけでなく周波数も知るためであるのに対し、ここで示す方法を使用するためには信号の周波数はあらかじめ正確にわかっていなければなりませんので、一般的にはここで示す方法はスペクトル計算の代わりにはなりません。
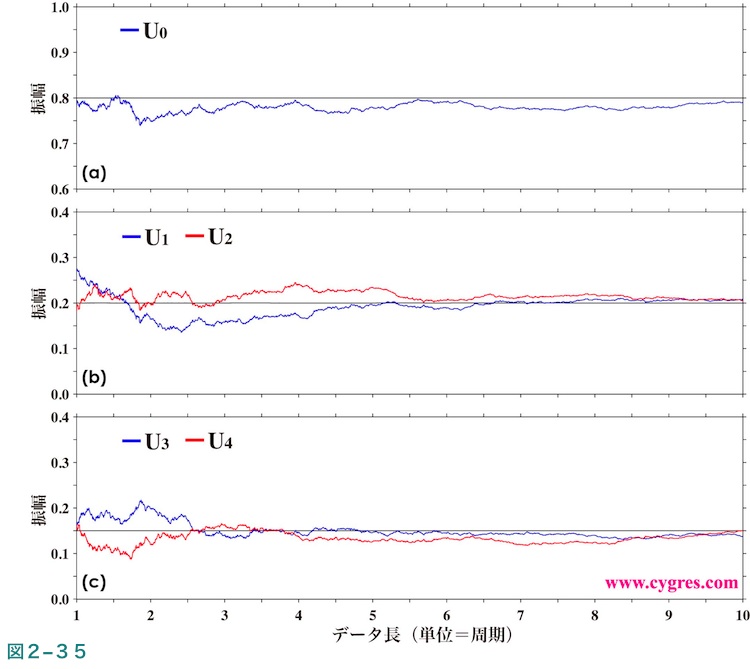
図2-35は図2-19に示すデータ(ノイズ小)よりこの方法で求めたU0、U1、U2、U3及びU4の振幅がデータが増えるにつれどのように変化するかを示す図で、図2-20に対応します。各図中の水平の黒の実線は実際の信号の振幅を示します。図2-35と図2-20を比較すると、この方法で計算した振幅はスペクトルより求めた振幅ほど大きく変動しないことがわかります。前述の”周波数一致に気を使う必要はありません”というのはこの点を意味しています。ただし、図2-20に現れている細かい振動を無視すると図2-35と図2-20には共通のパターンがあることがわかります。
図2-36は図2-31に示すデータ(ノイズ大)を使用した場合の図で、図2-32に対応する図です。両者の関係はノイズが小さい場合と同様です。