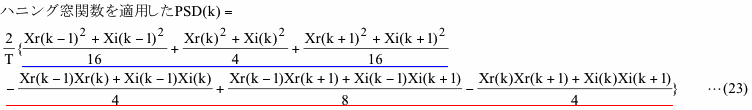お問合せは
->こちらへ<-

パワースペクトル密度計算 (スペクトル解析)
小額定型計算 PD001A/B
小額定型計算業務はお取り扱いするデータの形式、計算内容、計算結果の内容及び形式やデータ授受方法といった業務全般を定型化することでコスト削減及び納期短縮を図った計算サービスです。科学、技術研究のみではなく、商業や工業のいろいろな分野のデータの解析にご利用下さい。小額定型計算業務については->こちら<-をクリック下さい。
図を含む本文書の著作権はCygnus Research Internationalに帰属します。無断転載はお断り致します。
PD001A/B ユーザーガイド 5/7
目次
(1章) PD001シリーズの要約
(1-1) PD001シリーズで行う計算について
(1-2) お客様がご指定できる計算設定項目の要約
(1-2-1) トレンド除去; 全てのケースで個別に指定
(1-2-2) PSDの値の信頼区間のパーセンテージ; 全ケースで同一の値を指定
(1-2-3) テューキー窓関数のテーパー比; ケースB1、B2及びB3のみ適用 値は個別に指定
(1-2-4) 周波数領域での平滑化(以下FDSと略)ビン巾; ケースA1、B1及びC1の3ケースを除く全ケースで個別に指定
(1-3) 計算手法
(1-4) 入力データ(お客様のデータ)について
(1-5) プロダクツ
(1-5-1) 結果ファイル
(1-5-2) PDF形式の図
(1-6) 料金、納期およびご発注手順
(1-7) 個人情報、お客様のデータに関する情報保護
(2章) プロダクツの詳細及びその使用例
(2-1) 結果ファイル
(2-1-1) 結果ファイルのフォーマット(形式)
(2-1-2) 結果ファイルに記述する計算結果の内容
(2-1-2-1) 周波数 (Frequency)
(2-1-2-2) 周期 (Period)
(2-1-2-3) PSD (PSD)
(2-1-2-4) PSDの信頼区間 (Conf Int)
(2-1-2-5) 分散のパーセンテージ (% of Var)
(2-1-2-6) 振幅 (Amplitude)
(2-1-2-7) 位相 (Phase)
(2-1-3) 結果ファイルに書き出された情報の利用方法及び使用例
(2-1-3-1) 結果ファイルの値を用いて独自の図を作成したい場合
(2-1-3-2) PSD及びPSDの信頼区間の使用方法
(2-1-3-3) 特定の周波数での変動の巾(大きさ)を知りたい場合
(ケース1) 信号は振幅が一定の単一の周波数の三角関数で表される場合
(ケース2) 信号は振幅が一定の異なった周波数の三角関数を足し合わせたもので表される場合
(ケース3) 信号は単一の周波数の三角関数だが、振幅が時間とともに変動する場合
(ケース3-1) 信号の振幅の変動そのものが三角関数の形の場合
(例1) 信号は三角関数で周波数はf0。信号の振幅は周波数f1の三角関数の形で変動
(例2) 信号は三角関数で周波数はf0。信号の振幅は定数に周波数f1の三角関数を足し合わせた形で変動
(ケース3-2) 信号の振幅の変動そのものは三角関数ではない場合
(ケース4) 信号は周期的だが、三角関数の形ではない場合
(2-1-3-4) 特定の周波数域内の変動が全体の変動と比べてどの程度強いのかを知りたい場合
(2-1-3-5) 簡易デジタルフィルター(PD001Aのみ適用)
(2-1-3-6)データ中の値の変動の振幅を求める他の方法
(2-2)図
(3章) PD001シリーズ用のデータファイルの作成手順例
(4章) 各種指定項目の設定について
(4-1) トレンド除去;有無 無指定時は有
(4-1-1) トレンドとは? 除去の目的は?
(4-1-2) トレンド除去の例
(4-1-3) トレンド除去で問題が発生する例
(4-2) テューキー窓関数のテーパー比;%で表したテーパー比 無指定時は10%
(4-2-1) 窓関数を適用する理由
(4-2-2) 窓関数の適用とは
(4-2-3) ハニング窓関数;使用すると問題が生じる場合について
(4-2-4) 本小額定型計算業務 PD001Aでハニング窓関数を適用したPSDのみではなく、窓関数非適用及びテューキー窓関数を適用したPSDも計算する理由
(4-2-5) ハニング窓関数によるデータ両端近くの減衰を少なくする方法
(4-2-6) 窓関数が持つFDSに似た効果について
(4-2-7) IFDSは必ずしもPSDを平滑化しない
(4-2-8) 窓関数適用によるPSDや振幅スペクトル減衰に対する補正
(4-2-9) 窓関数適用時の補正の効果
(4-2-10) テューキー窓関数のテーパー比がPSDに与える影響
(4-3) 周波数領域での平滑化(FDS)ビン巾; 1、3、5、7等奇数 無指定時は無し(1)、3及び7
(4-3-1) PSDに対するFDS
(4-3-2) 振幅スペクトルに対するFDS
(4-3-3) FDSを適用した場合の周波数解像度
(4-3-4) FDSに代わる他の平滑化法
補足1 コンピュータを用いて計算をする際に生じる誤差について
補足2 パワースペクトル密度関数のスペクトル漏れと窓関数の関係について
補足3 データ長が短いと単一のピークが現れ、長いとツインピークが現れる理由
補足4 S1のトレンド除去により付加される直線成分のPSDの悪影響に対するS1とSRの周波数の関係
(4-2) テューキー窓関数のテーパー比;%で表したテーパー比 無指定時は10%
テューキー窓関数はテーパー比が0%の場合は窓関数を適用しないのと同じになり、テーパー比が100%の場合はハニング窓関数と同じになります。そこで、この節では最初に窓関数の一般的な事項に関して記述し、次にハニング窓関数に関して比較的詳しく記述します。そして最後の(4-2-10)にテューキー窓関数のテーパー比を変えるとPSDがどのように変わるかに関して記述します。
(4-2-1) 窓関数を適用する理由
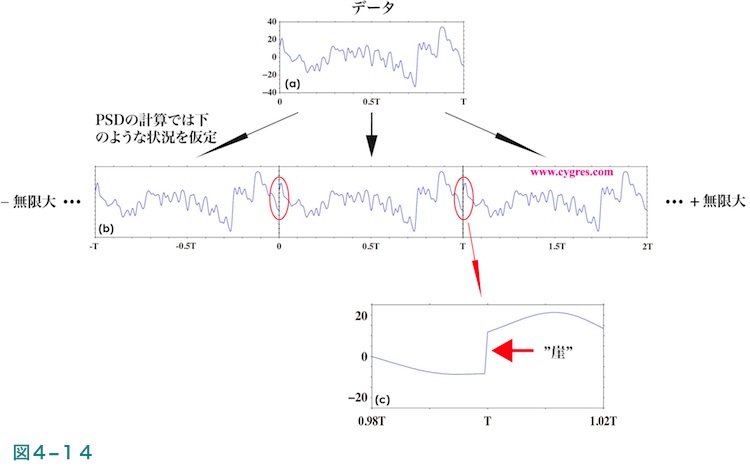
本小額定型計算業務PD001シリーズのように一般によく用いられる方法で限られた長さのデータよりPSDを計算する場合は、図4-14(a)に示すような手持ちの限られた長さのデータは図4-14(b)に示すようにそれが無限に繰り返される無限に長いデータの一部という仮定をおきます。PSDを計算する周波数(各ビンの周波数)はこの仮定により決められています。しかし、この仮定のために手持ちのデータの終了点と開始点が図4-14(b)の赤い楕円内で示すように繋がれるため、通常はそこで図4-14(c)に示すような不連続な”崖”ができてしまいます。このような不連続あるいは値のジャンプがあると、それを式(3)で示すように正弦波の和で表すためには多くの成分が必要となり、結果として広い周波数域でPSDの値が大きくなりスペクトル漏れが起きてしまいます。窓関数を適用するとこのような”崖”がなくなり、その結果としてスペクトル漏れが少なくなります。なお、窓関数とスペクトル漏れの関係については補足2にもう少し厳密に記述します。
(4-2-2) 窓関数の適用とは
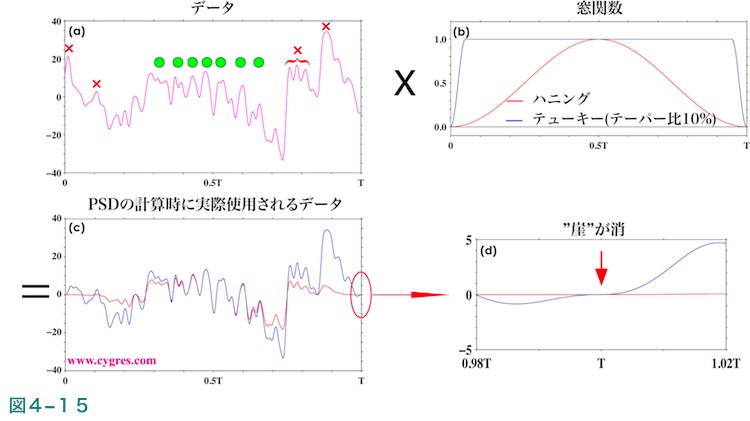
窓関数をデータに適用するということは、具体的には図4-15(a)で示すようなデータに図4-15(b)で示すような最小値0.0、最大値1.0の重みを掛けるということです。その結果は図4-15(c)のようになり、この値を使ってPSDを計算します。この操作により図4-15(d)に示すように”崖”がなくなります。なお、窓関数の最後の値は必ず0.0になりますので、PSDの計算に用いる最後のデータの値も0.0になります。
(4-2-3) ハニング窓関数;使用すると問題が生じる場合について
図4-15(b)(赤線)に示すようにハニング窓関数はデータの開始部分や終了部分を中央部分に比較してかなり減衰させる窓関数です。極端な表現をするとデータにハニング窓関数を適用すると、データの中央部付近の変動は重視されますが、そこから離れるにしたがいデータの変動は軽視されます。ここで、図4-15(a)に示すデータの場合、変動の様子が場所(時間)によってかなり変わっています。このため図4-15(a)の中央付近にある比較的安定した変動(緑色の丸)は図4-15(c)で見られるようにハニング窓関数を適用しても比較的減衰せずに残りますが、図4-15(a)の両端付近にある比較的大きな変動(赤色のバツ記号)はハニング窓関数を適用するとほぼ消滅してしまいます。なお図4-15(a)に示したデータはデモンストレーションのために人為的に作成したものではなく、図1-1(a)に示した実際のデータの一部で、見やすくするために低周波数域と高周波数域を除いた以外の操作は行っていません。
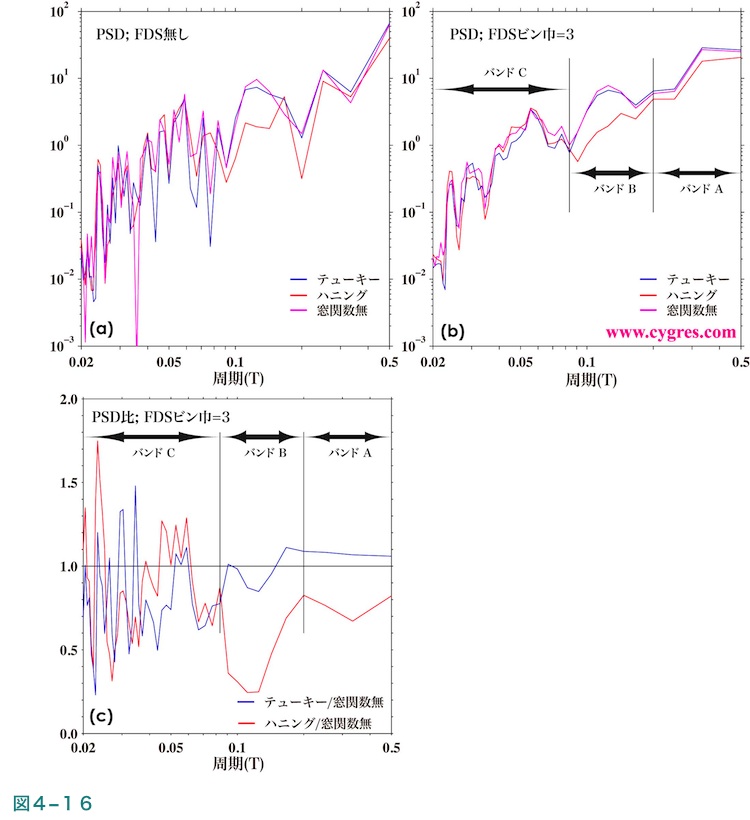
図4-16(a)は窓関数の適用でどのように図4-15(a)に示すデータのPSDが変わるかを示す図です。この図はやや見にくいので、平滑化巾3ビンのFDSを適用した結果を図4-16(b)に示します。これらの図によりバンドB内ではテューキー窓関数を適用したPSD(青線)や窓関数非適用のPSD(紫線)に比べハニング窓関数を適用したPSD(赤線)は明らかに小さくなっています。バンドAでも同様の傾向が見られます。ハニング窓関数を適用したPSDを窓関数非適用のPSDで割った値(赤線)及び、テューキー窓関数を適用したPSDを窓関数非適用のPSDで割った値(青線)を図4-16(c)に示しますが、この図でもバンドB及びバンドAでハニング窓関数を適用したPSDが他より小さくなっていることがわかります。
図4-17の左側の3図((a)、(c)及び(e))は図4-15(a)に示すデータを(2-1-3-5)で記述した方法によってバンド別に分離した結果で、右側の3図((b)、(d)及び(f))は左側に示す分離後のデータにそれぞれ個別にハニング窓関数を適用した結果です。ここで、本小額定型計算業務PD001シリーズを含めた通常のPSDの計算では式(3)が成立することを前提としていますので、式(3)中の複数の周波数成分をバンドとして纏めると
![]()
のように図4-15(a)に示すデータを表現することができます。したがって図4-17のようにバンド別に一旦分離してから個別にハニング窓関数を適用してその結果を足し合わせたものは分離前のデータにハニング窓関数を適用したものと同じになりますので、図4-17の左右の差を調べると何故バンドB及びバンドAでハニング窓関数を適用したPSDが他より小さくなったかがわかります。
ここで、データの変動の大きさの指標として前述したように変動の”エネルギー”を表す分散を用います。図4-17の左側の各図に記入している分散は元のデータをバンド別に分離した後に個別に計算した分散です。これに対し、図4-17の右側の各図に記入している補正後の分散というのはバンド別に分離した個別のデータにハニング窓関数を適用した後に計算した分散に(4-2-8)に記述する補正を適用したものです。なお、この補正は窓関数を適用したPSDに対し加える補正と同じもので、個々のデータに掛けられる窓関数の値が1.0以下なのでそれによる減衰を補正するために行います。図4-17の右側の各図に記入している分散比というのは右側の図の補正後の分散を左側の図の分散で割った値で、これによりハニング窓関数により実質どの程度各バンドのデータの変動が減衰したかがわかります。
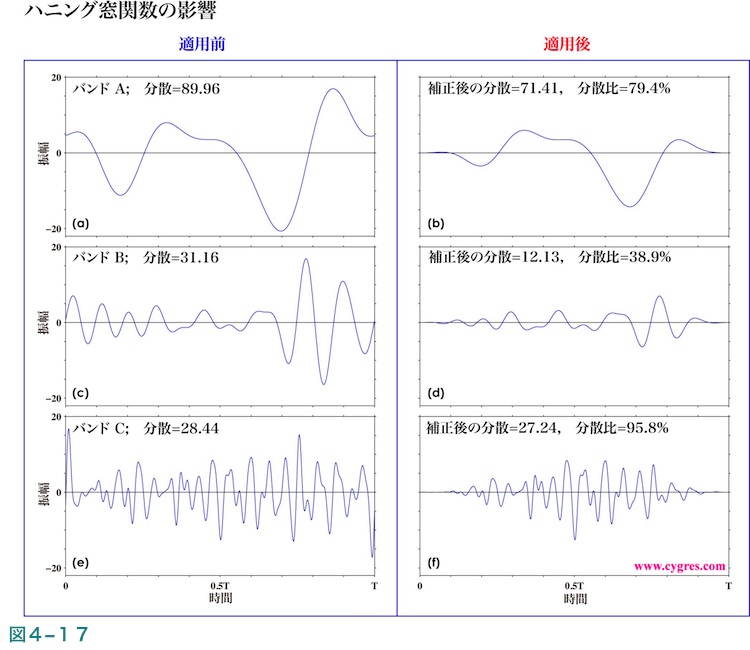
バンドBの変動は図4-17(c)が示すように主にデータの両端近くにあるのですが、これらの変動は図4-17(d)が示すようにハニング窓関数によって大きく減衰させられ、このバンドの分散比は僅か38.9%です。このためハニング窓関数を適用したPSDのバンドB内の値は窓関数非適用のPSDの値よりかなり小さくなっています。バンドAにも似たような傾向が見られます。これに対しバンドCの変動は図4-17(e)が示すようにデータのどの部分にも概ね一様な大きさで存在し、そのため図4-17(f)中の分散比が示すようにハニング窓関数による減衰は実質ほとんどありません。したがってこのバンドではハニング窓関数を適用したPSDと窓関数非適用のPSDは、細かい違いはありますが、概ね同じような大きさの値になっています。
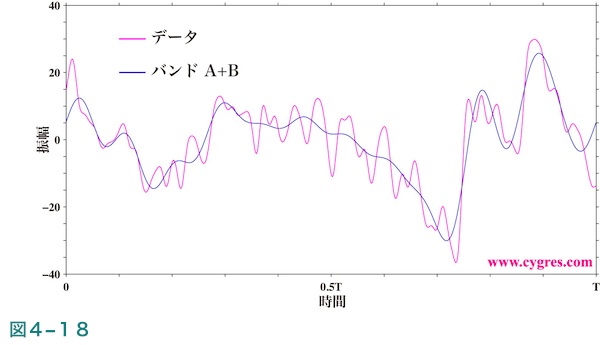
なお、これはこの節の記述にとって大事なことではないのですが、図4-18に示すようにバンドAとバンドBを足し合わせたもの(黒線)は元のデータ(紫線)の大雑把なプロフィールを再現しますので、少なくともこのデータに関してはバンドAとバンドBに含まれる変動は重要です。
(4-2-4) 本小額定型計算業務 PD001Aでハニング窓関数を適用したPSDのみではなく、窓関数非適用及びテューキー窓関数を適用したPSDも計算する理由
一般に工学や産業関連のデータに含まれる変動は、慣性等による意図しないものも含め何らかの制御がされたモーター、エンジンや、発振器によるものが多いので、データに含まれる変動の統計的な性格はデータのどの部分でも概ね同じようなものであることが多いことが予想されます。そのような場合は上に記述したように窓関数によってデータの中央部のみが重視されるようになってもそれが重大な問題になることはあまり無いと考えられます。しかし、人間の経済活動に関するデータ(株価等)や自然科学で扱うようなデータに含まれる変動の場合は上で示したようにデータに含まれる変動の統計的な性格がデータのどの部分をとるかによってかなり変わってくることが考えられます。このような場合には上で記述したような問題が起きる可能性があるのですが、PSDを実際計算してその結果を見てみないとそのような問題が生じているかどうかは普通はわかりませんので、PSDを計算する前に最善のPSDの計算の設定を決めるのは困難です。したがって、PD001Aではいろいろな設定で先にPSDを計算し、その結果を比較して最善のものをお客様にご利用いただくという方針を採用しています。
(4-2-5) ハニング窓関数によるデータ両端近くの減衰を少なくする方法
(この方法は本小額定型計算業務 PD001シリーズでは用いません)
ハニング窓関数は一般的にはよく使われる窓関数ですので、たとえこの窓関数で上に記述したような問題が発生するにしてもこの窓関数を使用したいという場合もあると考えられます。そこで、ここではこの窓関数を使用しつつデータ両端近くの減衰を少なくするウェルチの方法とよばれる方法について記述します。なお、この方法を使用すると結果ファイルの形式を変更する必要があることや、お客様がご指定可能な項目が複雑化しますので、本小額定型計算業務PD001シリーズにこの方法を含める予定はありません。ただし、ご要望が多ければ別の小額定型計算業務として提供致します。
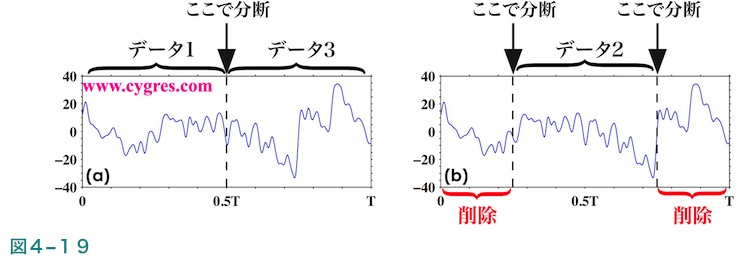
この方法を適用するためには最初に図4-19(a)に示すように元のデータセットを中央で分割します。これにより元のデータセットの半分の長さのデータセットが2個(データ1及びデータ3)できます。つぎに、図4-19(b)に示すように元のデータセットの最初の1/4の部分と最後の1/4の部分を削除しますと元のデータセットの半分の長さのデータセット(データ2)がさらにもう1個できます。
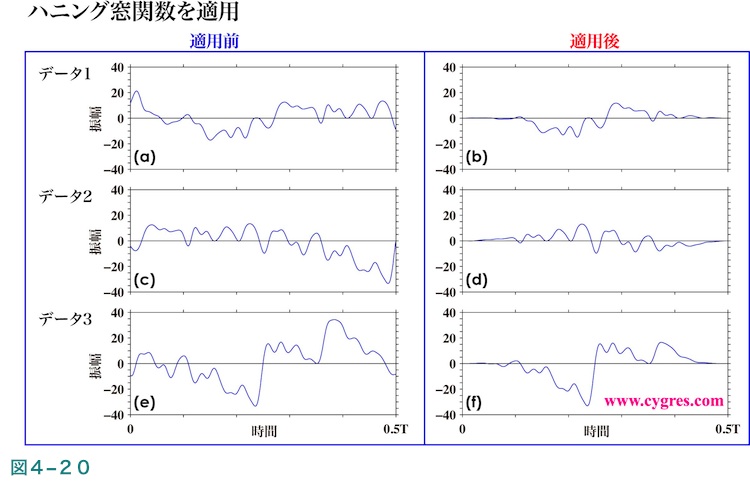
次に、これらの3個のデータセットに対し図4-20に示すように個別にハニング窓関数を適用した後にそれぞれのPSDを計算します。ここまでの操作により計3セットのPSDが計算されますが、これらの3個のデータセットのデータ長(数)は同じですので、計算された3セットのPSDのビンの数及び各ビンの周波数もすべて同じになります。最後にそれぞれのビンについて3セットのPSDの平均を計算します。
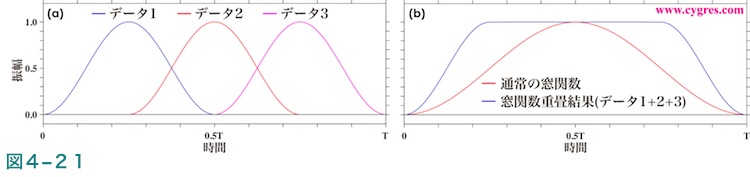
図4-21(a)に各データセットに掛けられるハニング窓関数の値、すなわち重みを、元のデータセットにおいてそれぞれのデータセットがどの部分(図の水平位置)にあたるかがわかるような形で示します。この図では各データセットの一部が重ね合わされていますが、ここでのポイントは一部のデータが複数回使われるのを許容することによりデータ両端近くの減衰を少なくできることです。図4-21(b)の青線は図4-21(a)の各線で表される重みを各データについて足し合わせた結果で、赤線は通常のハニング窓関数による重みを示します。この図の青線により、データセットの重ね合わせの結果全体の1/2のデータに掛けられる重みは実質1.0になることがわかります。なおこのケースでは全体の1/2のデータは2度使われることになります。
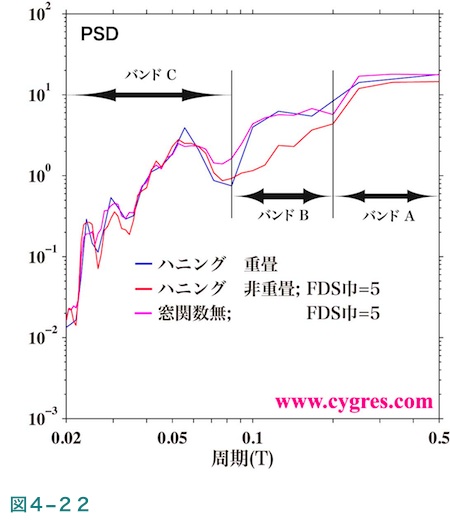
図4-22の青線はこの方法で計算したPSDを、赤線は通常のハニング窓関数を適用して計算したPSDを、紫線は窓関数を適用せずに計算したPSDを示します。この図の赤線及び紫線は図4-16(a)及び(b)で示した赤線及び紫線と同じPSDですが、ウェルチの方法(青線)を用いると平滑化が行われるため、それとあわせるために平滑化巾5ビンのFDSを適用しています。この図よりウェルチの方法を用いるとバンドA及びBにおいてもPSDはあまり減衰せず、窓関数非適用の結果と概ね同程度の値になることがわかります。
ウェルチの方法を用いるとここで記述したように便利な場合があるのですが、元のデータより短いデータセットを作成して計算するため、各ビンの周波数間隔が広くなるので周波数解像度が悪くなります。これは同時に周波数ゼロを除く最も低い周波数のビンの周波数が高くなることを意味しますので、低周波数の変動が重要である場合は注意が必要となります。
(4-2-6) 窓関数が持つFDSに似た効果について
窓関数を適用すると前述したようにFDSに似た効果(以下ではIFDSと略します)が生じます。IFDSはFDSのように必要に応じて細かな調整も可能な意図的に加えるものと異なり、データに窓関数を適用した時点で自動的に組み込まれてしまう効果で、調整は窓関数そのものを別のものに変える以外はできず、細かな調整は困難な効果です。この効果の説明を直感的にわかりやすい方法で行うのは困難ですので、この節では数式を比較的多用致しますが、もし本小額定型計算業務のご発注の検討をされる上で不明な点があるというような場合はご発注前にお問い合わせください。
ここでは、まずPSDがどのように算出されるのかという点から始めます。窓関数を適用しない場合の片側PSDは下の式のように算出されます。なお、下式の右辺の分子側にある数値2は片側PSDを採用したために必要になる係数です。

ここで、フーリエ変換の結果は一般に実数部と虚数部を含む複素数になりますが、上式右辺の分子の数値2より右の部分はこの実数部の自乗と虚数部の自乗を加えたものです。これに対し、窓関数を適用した場合の片側PSDは以下のようになります。

上の式は任意の周波数のPSDの値の式ですが、通常はデータ長が限られていますので一定間隔の周波数の値を算出します。この一定間隔の周波数のものをこれまではビンと呼んできましたので、この節でも同様にビンと称します。データx(t)のk番目のビンのフーリエ変換は
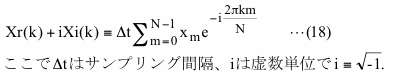
ここで、kはビンの番号で0からデータ数(N)/2迄の値、Xr(k)はフーリエ変換の結果の実数部で、Xi(k)はその虚数部です。なお、以下では添字rは実数部を、添字iは虚数部を意味します。厳密にはkはマイナスのデータ数/2からプラスのデータ数/2迄のように負の値も持てるのですが、ここでは正の周波数でのみ定義される片側PSDを使いますので、負のkの部分は無視します。式(18)を使うと窓関数非適用の場合のk番目のビンのPSDは下のようになります。
![]()
次に窓関数を適用した場合ですが、データx(t)に窓関数w(t)を掛けたもののフーリエ変換は畳み込み定理という定理によりx(t)のフーリエ変換の結果とw(t)のフーリエ変換の結果を畳み込んだものになります。ここで重要なのはこのx(t)のフーリエ変換の結果とw(t)のフーリエ変換の結果の畳み込みというものが、実際にはx(t)のフーリエ変換の結果に移動平均を適用したものと類似(厳密には重みの総和は1.0ではないので、”平均”ではないのですが)で、その移動平均の重みに相当するのがw(t)のフーリエ変換の結果になるという点です。以下に窓関数がハニング窓関数の場合についてもう少し具体的に記述します。
まず、式(18)と同様に窓関数のn番目のビンのフーリエ変換を下のように表します。
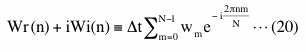
ただし、ここではnは負の値も可能でマイナスのデータ数/2からプラスのデータ数/2までの値をもちます。なお、この式の右辺のWは大文字で、左辺のwは小文字で、両者は同じではありません。ハニング窓関数はWi(n)は常にゼロでWr(n)はnが-1、0または+1以外の場合はゼロになるという大変便利な性格を持っていますので、ここでの例に採用しています。この便利な性格を利用し、データx(t)にハニング窓関数w(t)を掛けたもののk番目のビンのフーリエ変換を上述の畳み込みを具体的に行って求めると下のようになります。
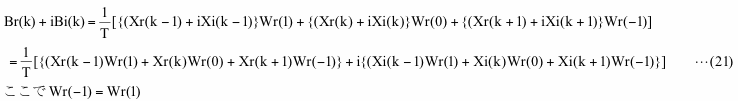
なお、kが0の場合はk-1はN/2に置き換え、kがN/2の場合はk+1を0に置き換えます。式(21)でWの値を重みと考えると、式(21)の右辺は実数部も虚数部もXrまたはXiの前後計3点の重み付き移動平均と類似の形になっています。ここで、ハニング窓関数の場合はWr(-1)=Wr(1)= -T/4、Wr(0)=T/2になりますので、これらの値を式(21)に代入すると、
![]()
のように非常に簡単な式になります。式(19)のXr(k)を式(22)のBr(k)に、式(19)のXi(k)を式(22)のBi(k)に置き換えると、ハニング窓関数を適用した場合のk番目のビンのPSDは結局下のようになります。
ここで、仮に信号のあるビンがk番目とすると、式(23)よりk-1番目のビンのPSDにもk+1番目のビンのPSDにもk番目のビンの値が影響しますが、それより離れたビンのPSDにはk番目のビンのPSDは何ら影響を与えません。図2-6、図4-6(a)や図4-10(c)でハニング窓関数を適用した場合は周波数一致が成立(データ長A)していても信号のピークが3ビンの巾に広がるのはこのためです。この信号の巾の拡大は原理的にはスペクトル漏れと同じなのですが(補足2)、通常はスペクトル漏れとは呼びません。なお、ハニング窓関数以外の窓関数を使用した場合はWr(n)もWi(n)も多くのnで0ではなくなるので、式(22)や式(23)のような簡単な式は得られません。図2-8(a)でテューキー窓関数を適用した結果(青線)のみ全周波数域で比較的大きな値をもつのはこのためです。
(4-2-7) IFDSは必ずしもPSDを平滑化しない
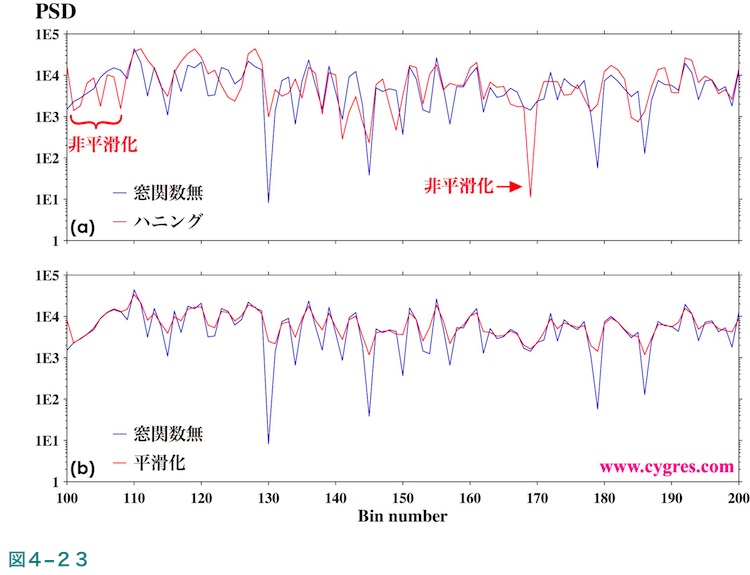
窓関数を適用すると一般的にはPSDは平滑化されるのですが、そうでない場合もあります。ここで、再びハニング窓関数を例として使用します。ハニング窓関数を適用した場合のPSDは式(23)のようになりますが、式(23)の右辺の上段部(青下線)は式(19)より窓関数非適用のPSDの単純な3点の重み付き移動平均と類似の形になっていることがわかります。したがってこの部分だけであればハニング窓関数を適用した場合のPSDは窓関数非適用のPSDに比べ常に滑らかになります。しかし式(23)の右辺の下段部(赤下線)は窓関数非適用のPSDとはまったく関係がありません。このため、この下段部の値が上段部の値に比べ無視できない大きさの場合はPSDはかえって非平滑化されることもあります。図4-23(a)にハニング窓関数を適用した場合のPSD(赤線)と窓関数非適用の場合のPSD(青線)を示します。この図よりハニング窓関数を適用すると滑らかになる部分が多いのですが、かえって変化が大きくなる部分(非平滑化)もあることがわかります。これに対し図4-23(b)の赤線に式(23)の右辺上段部のみで計算した結果を示しますが、この図でわかるように右辺上段部のみですとPSDは常に滑らかになります。なお、ウェルチの方法を用いた場合は式(23)の下段はXr(k-1)、Xr(k)、Xr(k+1)、Xi(k-1)、Xi(k)及びXi(k+1)間の相互相関に関連する値となりますが、PSDの計算に適用される一般的な統計理論によればこれらの項は非相関と考えられます。したがって多くのPSD結果を平均すると下段の値は小さくなり結果としてPSDがより平滑化されることが期待されます。
(4-2-8) 窓関数適用によるPSDや振幅スペクトル減衰に対する補正
窓関数を適用すると、PSDや振幅スペクトルの値は常に小さくなりますが、これは図4-15や図4-17で示されるように窓関数を掛けることによってデータの値がもとの値より小さくなるからです。本小額定型計算業務PD001シリーズでは窓関数を適用した場合は通常よく使われる方法でPSD及び振幅スペクトルの値を補正しています。具体的には下の式で示すCP及びCAを計算し、PSDにはCPを掛け、振幅スペクトルにはCAを掛けます。
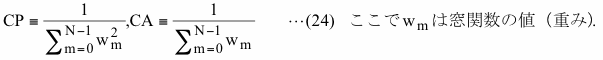
なお、この式で示されるように補正は窓関数の値のみから計算した定係数を用いますので、データそのものの特性に応じた周波数別の補正はできません。したがってこの補正では(4-2-3)で記述したようにデータそのものの特性が周波数によって変わることに対する補正はできません。
(4-2-9) 窓関数適用時の補正の効果
最初に振幅スペクトルについてですが、上述の補正がどの程度うまくできているのかを判断する目安としては補正後の値がどの程度実際の信号の値と一致するかというものが考えられます。この点については図2-7(a)、(b)及び(c)や図2-13(c)、図2-13(e)、図2-16等で示すように信号ビンの振幅に対する補正の効果は概ね良好と言えるようです。ただし、周波数一致が成立している場合は信号ビンの両隣のビンの振幅は実際の信号の場合はゼロになりますが、ハニング窓関数を適用した場合は図2-7(a)に示すように信号ビンの振幅の1/2になります。したがって、上述の補正により信号ビンの振幅を実際の信号の振幅と一致させると信号ビンの両隣のビンの振幅もそれに比例して大きくなりますので注意が必要です。
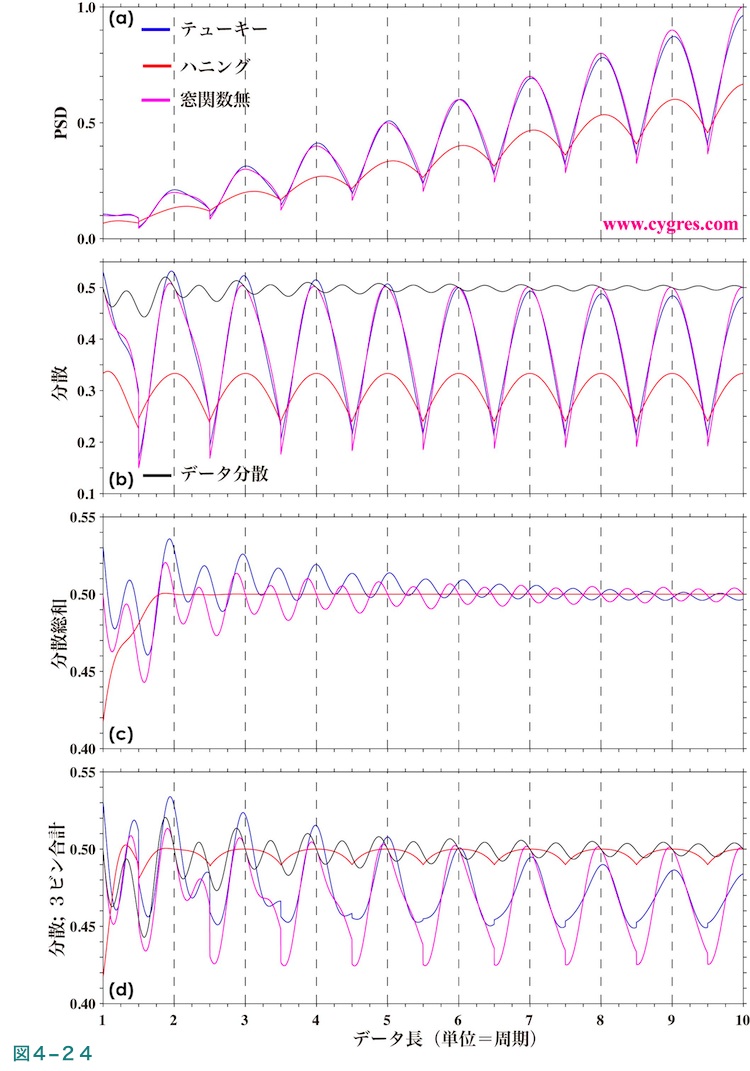
次にPSDですが、図4-24(a)は単一の周波数の信号のみを含むデータから計算した信号ビンのPSDがデータが増えるにつれどのように変化するかを示します。ここで使用したデータは図2-4で使用したものと同じで、この計算では(4-1-3)で記述したような問題を避けるためトレンド除去は行っていません。なお、窓関数を適用した場合(青線及び赤線)は上で記述した補正を行っています。この図よりデータが増えるにつれ信号ビンのPSDが増加しているのがわかりますが、これは図2-4(f)に示すようにデータが増えるにつれビンの周波数巾が狭くなるためです。図中の縦の黒の破線は周波数一致が成立しているデータ長を示します。
この図ではやや分かりにくいので、信号ビンのPSDにビンの周波数巾を掛けたもの、すなわち信号ビンの分散を図4-24(b)に示します。なお、図中の黒線はデータの分散です。ここで、上述の補正がPSDに対してどの程度うまくできているのかを判断する指標としては2つのものが考えられます。式(1)で示したように各ビンのPSDにビンの周波数巾を掛けたもの、すなわち各ビンの分散の総和はデータの分散になるのですが、窓関数を適用した場合はデータの変動が元のものより小さくなるために式(1)の左辺のデータは窓関数を適用する前の実際のデータのままで、右辺のPSDは窓関数適用後ですが未補正のPSDの値を使用すると等式が成立しなくなります。したがって、右辺側のPSDに適用する補正によって式(1)の左辺がどの程度窓関数を適用する前の実際のデータの分散に近づくのかという事が指標の1つになります。
PSDの補正がどの程度うまくできているのかを判断するもう1つの指標としては、振幅スペクトルの場合と同様に補正後の値がどの程度実際の信号の値に近いのかという事です。ここで示している例では信号は単一の周波数の三角関数のみですので、2番目の指標を用いると図4-24(b)中のデータの分散(黒線)と信号ビンの分散(黒以外の線)が一致することが望ましいと言えます。この図では窓関数非適用(紫線)及びテューキー窓関数を適用(青線)した場合は周波数一致が成立するデータ長でデータの分散と信号ビンの分散がほぼ一致していますが、ハニング窓関数を適用した場合は信号ビンの分散がかなり小さくなっています。したがって、これではハニング窓関数を適用した場合の補正は指標2を用いて判断すると補正に問題があるという結論になってしまいます。
しかし、このようにハニング窓関数を適用した場合に信号ビンの分散が小さくなるのは上で記述した補正に問題があるのではなく、式(23)で表されるようにハニング窓関数を適用すると、たとえ周波数一致が成立していても信号によるピークは信号ビンを中心とした3ビンの巾を持つものになるからです。ここで重要なのは窓関数とは無関係に式(1)が成立することが望ましい(ただし、左辺のデータは窓関数を適用する前の実際のデータのままで右辺のPSDは窓関数を適用した場合は補正後の値)という点です。窓関数非適用(紫線)及びテューキー窓関数を適用(青線)した場合は周波数一致が成立しているデータ長では信号ビン以外のビンのPSDは信号ビンのPSDに比べ相当小さい(窓関数非適用の場合は実質ゼロ)ので、データの分散は概ね信号ビンの分散に一致します。これに対し、ハニング窓関数を適用した場合は周波数一致が成立していても信号ビンの両隣のビンのPSDの値は信号ビンのPSDの1/4という大きな値となり、したがって信号ビンの両隣のビンを無視して信号ビンの分散のみを取り上げるとデータの分散より小さな値になっても当然ということになります。
図4-24(c)は各ビンの分散の総和を示します。なお、式(1)よりデータの分散は窓関数を適用しない場合の各ビンの分散の総和(紫線)と一致しますので、図では省略しています。また、この図の縦軸の表示範囲は図4-24(b)と比べてかなり狭くしていますので、ご注意ください。図4-24(c)より各ビンの分散の総和はハニング窓関数を適用した場合でも他と比べ特別に小さいわけではないことが分かります。図4-24(d)は信号ビン及びその両隣のビン、計3ビンの分散の和を示します。この図よりハニング窓関数を適用した場合の結果(赤線)は他の結果よりデータの分散(黒線)に近いことがわかります。特に周波数一致が成立しているデータ長(縦の黒の破線)ではハニング窓関数を適用した場合の結果もデータの分散もほぼ0.5(この場合の理論値)になっています。
これらの結果より窓関数を適用した場合のPSDに対する上述の補正は指標1を用いて判断する限り概ね良好で、指標1と指標2は矛盾する指標といえます。ただし、窓関数を適用した場合でも補正によって、左辺のデータは窓関数を適用する前の実際のデータのままで右辺のPSDは窓関数を適用した場合は補正後の値とした式(1)が完全に成立するならば、図4-24(c)ではすべての線がデータの分散(青線の窓関数非適用の結果と同じ)に一致しなければなりませんが、実際にはそうなっていません。また、図4-20で示したように周波数によって補正の効果がかなり変わってくる場合もあります。そういった点ではこの補正には限界があります。
(4-2-10) テューキー窓関数のテーパー比がPSDに与える影響
結論から先に述べますと、テーパー比を小さくすると周波数解像度が増し、テーパー比を大きくするとPSDや振幅スペトルの値がより精確になります。ただし、データが(4-2-3)で記述したようなものである場合はテーパー比を大きくすると(4-2-3)で記述したような問題が顕在化します。これらの詳細は以下に記述します。
まず、テーパー比が何であるのかという点ですが、図4-25は例としてテーパー比が50%のテューキー窓関数の値を示します。この窓関数をデータに適用すると、データの初めの25%及び終わりの25%の部分がこの図に示すような割合で減衰させられますが、中央部の50%は元の値のままになります。前述したようにテーパー比が0%ですと、データのどの部分も変わらないので窓関数非適用と同じになりますし、テーパー比が100%の場合はハニング窓関数と同じになります。
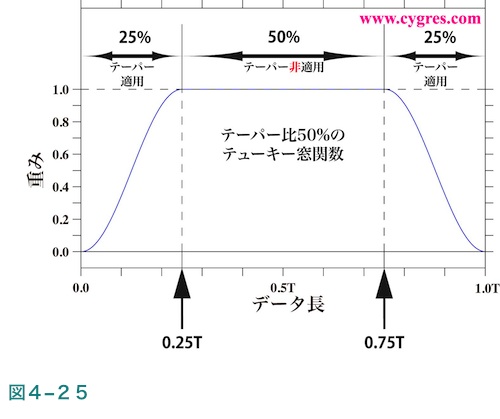
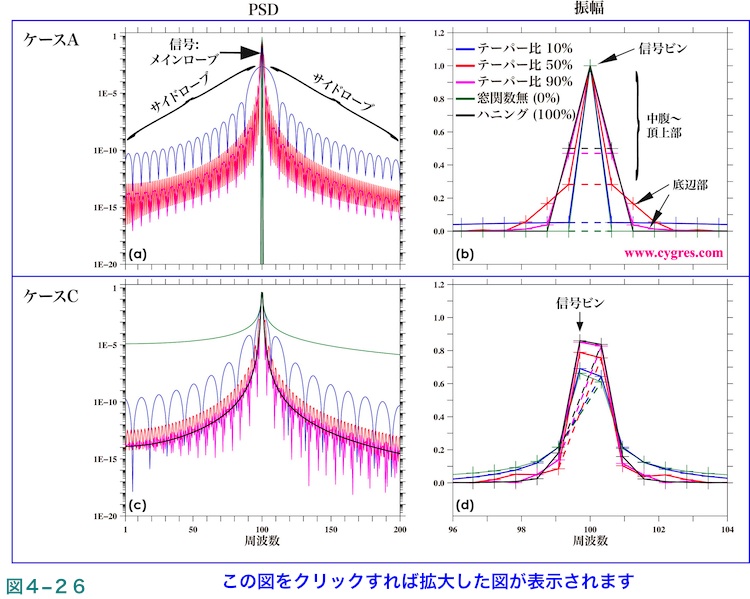
図4-26(a)はテーパー比10%のテューキー窓関数(青線)、テーパー比50%のテューキー窓関数(赤線)、テーパー比90%のテューキー窓関数(紫線)、ハニング窓関数(テーパー比100%のテューキー窓関数と同等;黒線)を適用した場合及び窓関数非適用の場合のPSD(テーパー比0%のテューキー窓関数と同等;緑線)の信号周辺部分を示します。これらの計算に使用したデータは単一の周波数の三角関数の信号のみを含むデータで、周波数以外は図2-4(a)に示すものと同じです。また、データ長は図2-4(a)のAに相当する長さで、周波数一致が成立しています。したがって、窓関数非適用の場合のPSD(緑線)は信号ビンのみ値を持ち、他のビンのPSDは実質ゼロとなり、また窓関数適用の場合も含めスペクトル漏れはおきていません。テーパー比が10、50及び90%のテューキー窓関数を適用した場合のPSDには信号ビンを中心として両側に丘上の多数のピークが現れますが、こういった部分はサイドローブと呼ばれます。このサイドローブが現れる原因は前述したように式(20)においてハニング窓関数と異なり多数のnでWr(n)及びWi(n)が0ではなくなるために信号の影響が信号ビン以外のビンに広く波及するからで、補足2に記述するように原理的にはスペクトル漏れと同種のものです。なお、サイドローブの大きさ(図では高さ)は横軸に均等スケールを採用すると信号ビンを中心として高低(図では左右)対称となり、テーパー比を大きくすると小さくなります。
図4-26(b)はこの場合の振幅スペクトルの信号ビン周辺のみを拡大した図で、この部分はメインローブと呼ばれます。この図ではメインローブ部の”山”の形状を示すために信号ビンの両隣のビンの値の間に色のついた破線を描画しています。この図よりテーパー比を大きくするにつれ色のついた破線の高さが高くなるので、信号ビンに隣接するビンの値が大きくなることがわかります。また、同時にこの”山”の中腹〜頂上部の巾が広くなります。この”山”の底辺部の巾についてはやや複雑です。このように周波数一致が成立する場合は、図4-26(a)で示すようにテーパー比を大きくしたほうが全般的にはサイドローブの値が小さくなるので信号がシャープになるのですが、図4-26(b)のようにメインローブのみを見るとテーパー比を小さくした方が局地的にはシャープになります。
図4-26(c)は実際の信号の周波数が信号ビンの周波数から最も離れるようなデータ長の場合(図2-4のデータ長Cに相当)であること以外は図4-26(a)と同じ図です。この場合は強いスペクトル漏れが生じますので、その結果として窓関数非適用のPSD(緑線)は全周波数域で大きな値になります。テーパー比が10(青線)、50(赤線)及び90%(紫線)のテューキー窓関数を適用した場合のサイドローブ部のPSDの値の大雑把な大きさは図4-26(a)と大差はありませんが、サイドローブの形状は変わっています。ハニング窓関数(黒線)を適用した場合は丘上のサイドローブは現れませんが、信号ビン以外のビンのPSDはテーパー比90%のテューキー窓関数を適用した結果と近い値になっています。図4-26(d)はこの場合の振幅スペクトルの信号ビン周辺のみを拡大した図で、データ長が異なる以外は図4-26(b)と同じ図です。この図よりテーパー比が大きくなるにつれ信号ビンの振幅が実際の信号の振幅(1.0)に近づくことがわかります。ただし、同時に信号ビンの隣のビンの振幅も大きくなり、 メインローブ部の”山”の頂上がより平坦になります。
以上より、テーパー比を小さくすると周波数解像度が増してメインローブ部がよりシャープになり、テーパー比を大きくすると計算されたPSDの値がより実際の信号のPSDに近づきます。
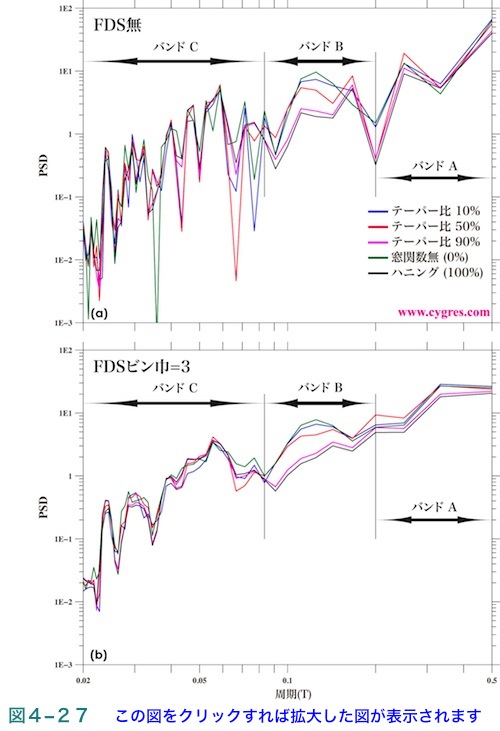
図4-27(a)は図4-15(a)に示した実際のデータに対し、テーパー比10%のテューキー窓関数(青線)、テーパー比50%のテューキー窓関数(赤線)、テーパー比90%のテューキー窓関数(紫線)、ハニング窓関数(黒線)を適用した場合のPSD及び窓関数を適用しなかった場合のPSD(緑線)を示します。図中のバンドは図4-16に示すものと同じです。この図はそれぞれの結果の比較を行うためには複雑すぎるので、平滑化巾3ビンのFDSを適用した結果を図4-27(b)に示します。この図よりそれぞれの結果の差がもっともはっきりと現れるのはバンドBですが、これはテューキー窓関数のテーパー比を大きくするにつれ(4-2-3)に記述したような問題が次第に顕在化してくるからです。その点を除外すると全般的にはテーパー比を変えた事によるPSDの違いはあまり大きくないと言えるようです。また、このように色々な周波数の信号やノイズが混在するデータでは図4-26のように窓関数のサイドローブがPSD上に現れることはあまりありません。
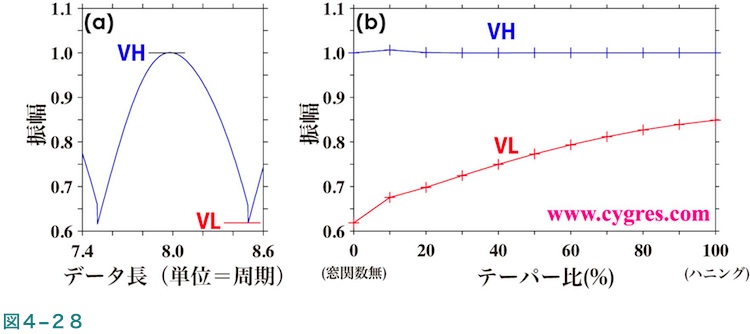
図4-28(a)は計算された信号ビンの振幅がデータ長が増えるにつれどのように変化するかを示した図2-4(b)の一部を取り出した図で、図中のVHは周波数一致が成立している場合の値を、VLは信号ビンの値が最も小さくなる値を示します。図4-28(b)はこのVHとVLがテーパー比を変えるとどのように変わるかを示します。実際のデータを取り扱う場合は周波数一致を成立させるのは困難ですので両者の差が小さいほうが好ましいのですが、この図よりテーパー比を大きくしたほうが差が小さくなることがわかります。
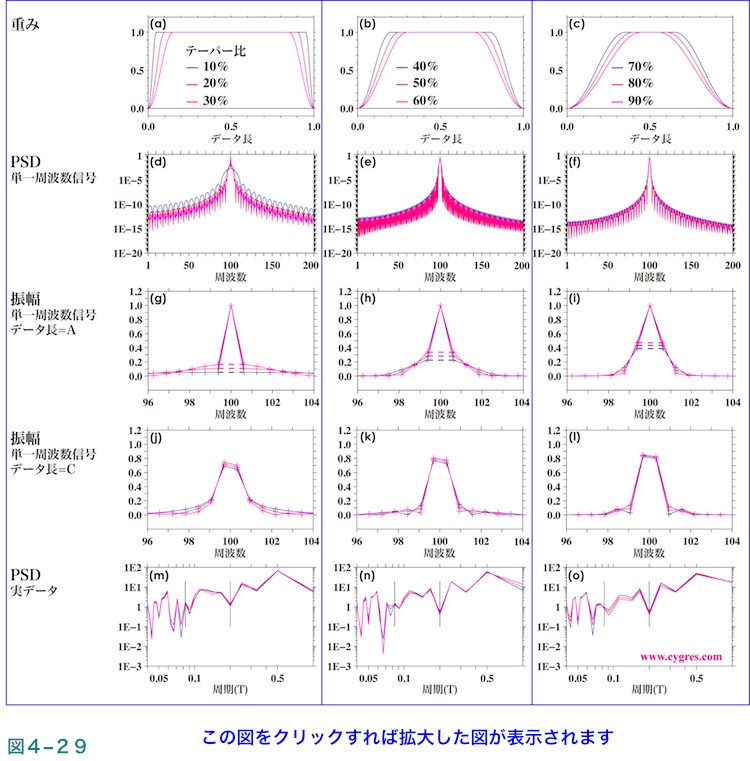
最後に10%から90%まで10%刻みでテーパー比を変えるとPSD及び振幅スペクトルがどのように変わっていくかを図4-29に示します。この図の一番上の段((a)、(b)及び(c))はそれぞれのテーパー比のテューキー窓関数の値(データにかける重みに相当)を、2番目の段((d)、(e)及び(f))は図4-26(a)と同様に単一の周波数の三角関数のみを含むデータで周波数一致が成立している場合のPSDを、3番目の段((g)、(h)及び(i))は図4-26(b)と同様に単一の周波数の三角関数のみを含むデータで周波数一致が成立している場合のメインローブ周辺の振幅スペクトルを、4番目の段((j)、(k)及び(l))は図4-26(d)と同様に単一の周波数の三角関数のみを含むデータで周波数一致が成立していない場合のメインローブ周辺の振幅スペクトルを、最下段((m)、(n)及び(o))は図4-27(b)と同様に実際のデータを使用し平滑化巾3ビンのFDSを適用したPSDを示します。なお、図は3段階の異なるテーパー比の結果を1グループとして列別に分け、それぞれの列のテーパー比は最上段の図中に記入しています。