お問合せは
->こちらへ<-

パワースペクトル密度計算 (スペクトル解析)
小額定型計算 PD001A/B
小額定型計算業務はお取り扱いするデータの形式、計算内容、計算結果の内容及び形式やデータ授受方法といった業務全般を定型化することでコスト削減及び納期短縮を図った計算サービスです。科学、技術研究のみではなく、商業や工業のいろいろな分野のデータの解析にご利用下さい。小額定型計算業務については->こちら<-をクリック下さい。
図を含む本文書の著作権はCygnus Research Internationalに帰属します。無断転載はお断り致します。
PD001A/B ユーザーガイド 7/7
目次
(1章) PD001シリーズの要約
(1-1) PD001シリーズで行う計算について
(1-2) お客様がご指定できる計算設定項目の要約
(1-2-1) トレンド除去; 全てのケースで個別に指定
(1-2-2) PSDの値の信頼区間のパーセンテージ; 全ケースで同一の値を指定
(1-2-3) テューキー窓関数のテーパー比; ケースB1、B2及びB3のみ適用 値は個別に指定
(1-2-4) 周波数領域での平滑化(以下FDSと略)ビン巾; ケースA1、B1及びC1の3ケースを除く全ケースで個別に指定
(1-3) 計算手法
(1-4) 入力データ(お客様のデータ)について
(1-5) プロダクツ
(1-5-1) 結果ファイル
(1-5-2) PDF形式の図
(1-6) 料金、納期およびご発注手順
(1-7) 個人情報、お客様のデータに関する情報保護
(2章) プロダクツの詳細及びその使用例
(2-1) 結果ファイル
(2-1-1) 結果ファイルのフォーマット(形式)
(2-1-2) 結果ファイルに記述する計算結果の内容
(2-1-2-1) 周波数 (Frequency)
(2-1-2-2) 周期 (Period)
(2-1-2-3) PSD (PSD)
(2-1-2-4) PSDの信頼区間 (Conf Int)
(2-1-2-5) 分散のパーセンテージ (% of Var)
(2-1-2-6) 振幅 (Amplitude)
(2-1-2-7) 位相 (Phase)
(2-1-3) 結果ファイルに書き出された情報の利用方法及び使用例
(2-1-3-1) 結果ファイルの値を用いて独自の図を作成したい場合
(2-1-3-2) PSD及びPSDの信頼区間の使用方法
(2-1-3-3) 特定の周波数での変動の巾(大きさ)を知りたい場合
(ケース1) 信号は振幅が一定の単一の周波数の三角関数で表される場合
(ケース2) 信号は振幅が一定の異なった周波数の三角関数を足し合わせたもので表される場合
(ケース3) 信号は単一の周波数の三角関数だが、振幅が時間とともに変動する場合
(ケース3-1) 信号の振幅の変動そのものが三角関数の形の場合
(例1) 信号は三角関数で周波数はf0。信号の振幅は周波数f1の三角関数の形で変動
(例2) 信号は三角関数で周波数はf0。信号の振幅は定数に周波数f1の三角関数を足し合わせた形で変動
(ケース3-2) 信号の振幅の変動そのものは三角関数ではない場合
(ケース4) 信号は周期的だが、三角関数の形ではない場合
(2-1-3-4) 特定の周波数域内の変動が全体の変動と比べてどの程度強いのかを知りたい場合
(2-1-3-5) 簡易デジタルフィルター(PD001Aのみ適用)
(2-1-3-6)データ中の値の変動の振幅を求める他の方法
(2-2)図
(3章) PD001シリーズ用のデータファイルの作成手順例
(4章) 各種指定項目の設定について
(4-1) トレンド除去;有無 無指定時は有
(4-1-1) トレンドとは? 除去の目的は?
(4-1-2) トレンド除去の例
(4-1-3) トレンド除去で問題が発生する例
(4-2) テューキー窓関数のテーパー比;%で表したテーパー比 無指定時は10%
(4-2-1) 窓関数を適用する理由
(4-2-2) 窓関数の適用とは
(4-2-3) ハニング窓関数;使用すると問題が生じる場合について
(4-2-4) 本小額定型計算業務 PD001Aでハニング窓関数を適用したPSDのみではなく、窓関数非適用及びテューキー窓関数を適用したPSDも計算する理由
(4-2-5) ハニング窓関数によるデータ両端近くの減衰を少なくする方法
(4-2-6) 窓関数が持つFDSに似た効果について
(4-2-7) IFDSは必ずしもPSDを平滑化しない
(4-2-8) 窓関数適用によるPSDや振幅スペクトル減衰に対する補正
(4-2-9) 窓関数適用時の補正の効果
(4-2-10) テューキー窓関数のテーパー比がPSDに与える影響
(4-3) 周波数領域での平滑化(FDS)ビン巾; 1、3、5、7等奇数 無指定時は無し(1)、3及び7
(4-3-1) PSDに対するFDS
(4-3-2) 振幅スペクトルに対するFDS
(4-3-3) FDSを適用した場合の周波数解像度
(4-3-4) FDSに代わる他の平滑化法
補足1 コンピュータを用いて計算をする際に生じる誤差について
補足2 パワースペクトル密度関数のスペクトル漏れと窓関数の関係について
補足3 データ長が短いと単一のピークが現れ、長いとツインピークが現れる理由
補足4 S1のトレンド除去により付加される直線成分のPSDの悪影響に対するS1とSRの周波数の関係
(4)スペクトル漏れを除去する他の計算方法(本方法をPD001A/Bに含める予定はありません)
PSDを計算する方法としてPD001A/Bで採用している方法以外に近年は最大エントロピー法(以下MEMと略)という方法も比較的よく用いられています。この節では図4-9(a)に示した微弱な信号SRと図4-9(c)に示したような非常に強い三角関数の信号S1を用いてS1からのスペクトル漏れについてPD001A/Bの結果とMEMの結果の違いを示します。MEMには細部で異なった幾つかの方法がありますが、ここではバーグ法とよばれる方法のみを用います。なお、現在のところMEMをPD001A/Bに含める予定はありません。
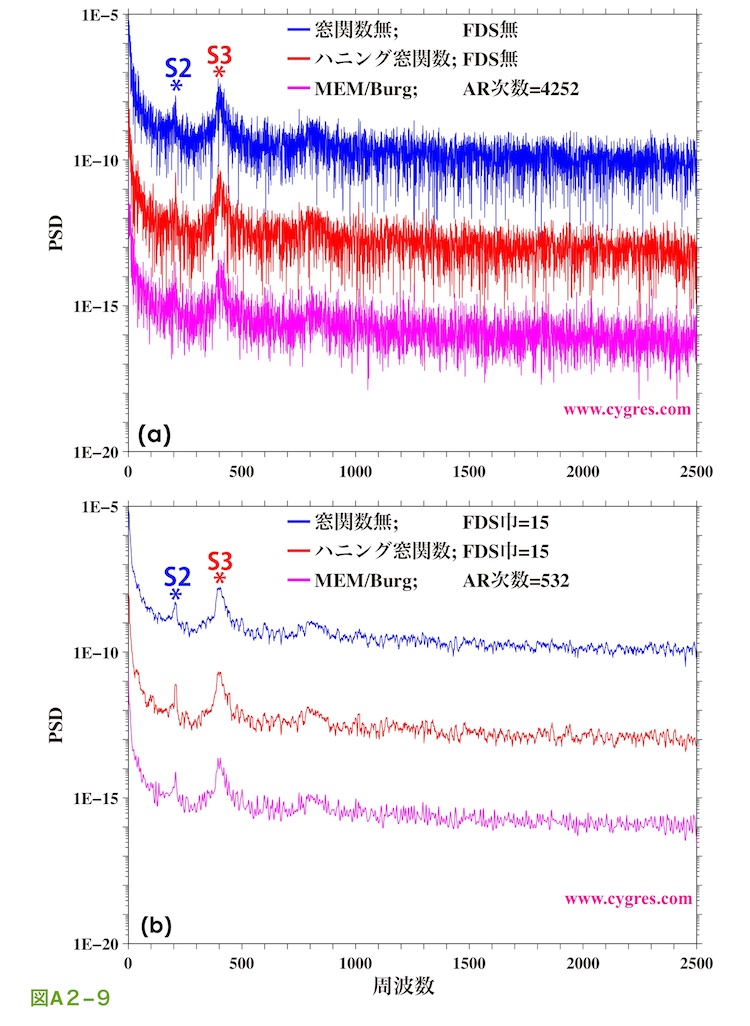
まず最初にSRのような種々雑多な信号やノイズを含むデータのPSDはPD001A/Bを用いてもMEMを用いても基本的にはどちらもPSDという同じものを求めようとしていますので、概ね同じような結果になる事を示します。図A2-9(a)及び(b)にPD001A/B(青線及び赤線)及びMEM(紫線)で計算したSRのPSDを示します。なお、図中の青線及び赤線は見やすくするために上方へ移動させています。この計算で使用したSRのデータ長は8514個で、このデータ長はS1を付加しPD001A/BでPSDを計算した場合にはS1のスペクトル漏れが最大に近くなるデータ長で、図A2-3の窓関数巾Bまたは図2-4(b)のデータ長Cに相当します。なお、S1を付加した場合にトレンドを除去すると(4-1-3)で記述したような問題が生じるため、ここで示した計算ではトレンド除去は行っていません。この図中のS2及びS3というのは図4-9の説明で記述したようにSRの開始から終了まで比較的安定して存在している潮汐成分によるピークで、ここでも目印として使用します。
ここで、図A2-9(a)の青線は窓関数を適用しなかった場合の結果で(矩形窓関数適用と同等)、水平軸に均等(線形)スケールを採用していることと線の位置を上方にずらしている以外は図4-13(a)の黒線と同じです。また、この図の赤線はハニング窓関数を適用した場合の結果で、水平軸のスケールや縦位置の違い以外は図4-13(c)の黒線と同じです。図A2-9(a)の青線や赤線と図A2-9(b)の青線や赤線との違いは、図A2-9(a)はFDS(周波数領域平滑化)を行わなかった場合の結果を示し、図A2-9(b)はFDSを適用した場合の結果を示している点です。(4-3)節で記述したようにFDSにはPSDを平滑化する効果があり、そのために図A2-9(b)には図A2-9(a)にあるような細かい変動がなく、全体の大雑把な様子が把握しやすくなっています。
MEMを用いてPSDを計算する際には自己回帰モデルの次数というものを決めなければいけませんが、この自己回帰モデルの次数はPSDの実質上の周波数分解能に影響を与えます。図A2-9(b)に示したPD001A/Bの結果(青線及び赤線)はFDSによって実質上の周波数分解能を図A2-9(a)に示した結果より下げていますので、MEMの方(紫線)もそれに応じて図A2-9(b)の自己回帰モデルの次数を図A2-9(a)のものより少ない値にしています。なお、MEMを使用する場合は任意の周波数でPSDを計算できますが、この節ではMEMの結果とPD001A/Bの結果を比較しますので、図A2-9ではPSDを計算する周波数はPD001A/BによるPSDの周波数と同じにしています。
図A2-9よりPD001A/Bを用いてもMEMを用いてもSRのような種々雑多な信号やノイズを含むデータよりPSDを計算すると全体の大雑把な様子は同じようなものになることがわかりますが、両者の結果の違いはこのような全体の大雑把な部分ではなく細部に顕われます。具体的にはS3についてMEMで計算した結果をよく見るとS3には複数のピークがあるように見えますが、S3は半日(12時間)周期の潮汐成分で、半日周期の潮汐というものには周期が少しずつ異なる複数のものがありますので、MEMの結果のほうがより精確なPSDを示している可能性があります。その他、詳細なスペクトル解析を行う場合はPD001A/BによるPSDとMEMによるPSDの違いは重要になることもありますが、本節はS1のスペクトル漏れの違いを示すことを目的としていますので、SRのPSDについてはどちらの方法を用いても概ね同じになるという点に留めます。
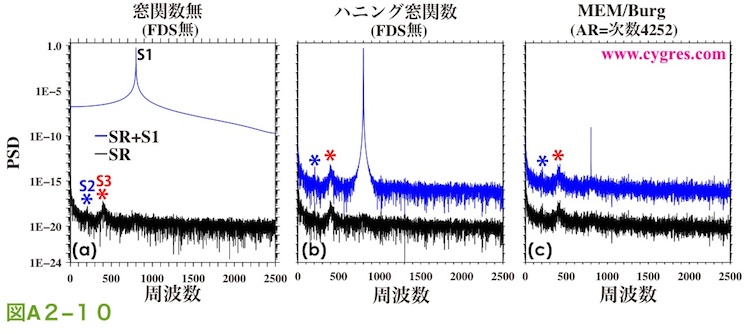
図A2-10の青線はSRにS1を付加して計算したPSD、黒線はSRのみの場合のPSDで、比較のために黒線は下方向にずらしています。図A2-10(a)及び図A2-10(b)はともにPD001A/Bで計算した結果ですが、図A2-10(a)は窓関数を適用しなかった場合でこの図の青線は図4-13(a)の青線と水平軸のスケール以外は同じで、図A2-10(b)はハニング窓関数を適用した場合の結果でこの図の青線は図4-13(c)の青線と水平軸のスケール以外は同じです。なお、両図の黒線は線の位置を上にずらしている以外はそれぞれ図A2-9(a)の青線及び赤線と同じです。図A2-10(c)はMEMで計算した結果で黒線は図A2-9(a)の紫線と同じです。なお、これらのPSDを計算する際にはトレンド除去は行っていません。
窓関数を適用せず(矩形窓関数適用と同等)にPD001A/BでPSDを計算すると図A2-10(a)よりS1のスペクトル漏れでSRのPSDはまったくわからなくなることがわかります。ハニング窓関数を適用すると図A2-10(b)よりS1のスペクトル漏れの影響はかなり抑えられ、比較的広範囲の周波数域でSRのPSDが確認できるようになることがわかります。これらに対しMEMは窓関数の畳み込みが行なわれませんので、図A2-10(c)よりスペクトル漏れが起きていないことがわかります。
ここでSRではなくS1に注目すると、図A2-10(a)や図A2-10(b)のS1のPSDの値はS1の実際のPSDの値にかなり近いものになっています。これに対し図A2-10(c)のPSDの値はS2やS3等SRのPSDは図A2-10(a)や図A2-10(b)の値とあまり変わらないにも関わらず、S1の値は他と比べ5億分の1程度(図の縦軸は対数スケールです)と、かなり小さくなっています。これは主にS1は振幅、位相や周波数が一定の三角関数でその理論的なスペクトルはS1の周波数のみ値がゼロでない線状のスペクトルですが、この図の作成のために計算した周波数の中にはS1の周波数に近いものはあっても一致する周波数はなかったためです。この点をもう少し明らかにするために自己回帰モデルの次数はそのままにし、PSDを計算する周波数間隔のみを小さくし、計算する周波数にS1の周波数を含めるようにして再計算した結果を図A2-11に示します。なお、図A2-11で表示している周波数範囲は785から815迄です。
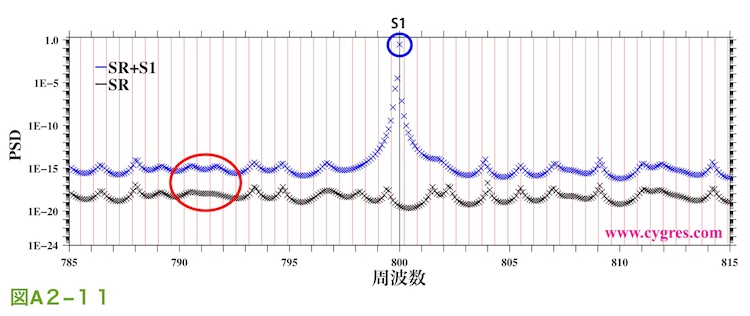
この図での青や黒のx印は再計算結果で、計算した周波数を明確にするためにこの図では各x印を直線で繋ぐことは行っていません。この図の縦の赤線は図A2-10でPSDを計算した周波数を示し、中央にある縦の黒線はS1の周波数を示します。このS1の周波数でのPSDは青の円で囲んだx印で、この値はS1の実際のPSDの値にかなり近いものになっています。理論的にはS1のPSDはS1の周波数以外ではゼロになるのですが、スペクトル漏れがないMEMでもこの図に示すようにS1は多少の周波数巾をもった”山”のような形になります。したがってS1のような強力な信号を見落とす可能性は低いのですが、この図よりMEMを使用してS1のような振幅、位相や周波数が一定の三角関数で表されるような信号のPSDの値を精確に知りたい場合はPSDを計算する周波数について注意を払う必要があることがわかります。もしS1の振幅がS2やS3と同程度の場合はS1を見落としてしまう可能性もあります。なお、信号の周波数は一定でも振幅が多少とも変動するような場合は(2-1-3-3)の(ケース3)で示したように信号の理論的なPSDのピークそのものが単一の周波数での線状のものではなくある程度周波数巾をもった”山”のようなものになります。
図A2-11の青や黒のx印で見られるような”丘”や”谷”の水平スケールは図中の縦の赤線の間隔と概ね同じで、図A2-11の青や黒のx印の水平間隔にくらべかなり大きくなっています。これはMEMの実質的な周波数分解能は自己回帰モデルの次数で決まり、その上限はデータのサンプリング間隔及びデータ数で決まってしまうためで、この図のように細かい周波数間隔でPSDを計算しても、ピークの周波数をより精確に知るためには役にたちますが、計算されたPSDの周波数分解能が向上するわけではありません。その他、MEMではこの補足で示したようなスペクトル漏れはおきませんが、図の赤の楕円で示した部分のようにS1の”山”から少し離れたところでもS1の影響が顕われています。
なお、MEMはPD001A/Bのようにデータは三角関数の和で表される(式(3))という仮定を用いませんので、データがS1のような振幅や周波数が一定の三角関数のみを含むような場合は想定外の結果を生じることがあります。当事業所は精確なスペクトル解析を行う必要がある場合は複数の手法でPSDを計算して相互比較することをお薦めしています。
補足3 データ長が短いと単一のピークが現れ、長いとツインピークが現れる理由
(2-1-3)のケース3-1の例1で信号の振幅の変動そのものが三角関数の形の場合はデータ長が短い場合はPSDには単独のピークが現れ、データ長が長い場合は2つのピーク(ツインピーク)になると記述しましたが、このような結果になることは数学的には2つの関数(S0とS1)の積(式(4)の青下線部)のフーリエ変換は個々の関数のフーリエ変換の畳み込みに等しいという畳み込み定理で説明できます。なお、ここでいきなりフーリエ変換を持ち出しましたが、これは(4-2-6)で記述したようにPSD及び振幅スペクトルはデータのフーリエ変換の結果を用いて計算するからです。
データ長がS1の周期に比べ短い場合は、S1の周波数f1に比べフーリエ変換の結果のビンの周波数巾が大きいためf1は周波数ゼロの最初のビンに含まれることになり、結果としてS1のフーリエ変換結果のピークは周波数ゼロの最初のビンに生じることになります。このような場合はS0のピークは畳み込みを行ってもそのままは元の周波数f0に残り、PSDや振幅スペクトルには周波数f0に単一のピークが現れます。この段階ではデータは緩やかに振幅が変わるS0と見なすことができます。ただし、この段階のデータ長はS1の周期を基準にすると短いのですが、図2-11に示すようにSLやSHの周期に比べればかなり長いと言えます。
データ長を長くしていくと、フーリエ変換の結果のビンの周波数巾が次第に小さくなり、ある段階でf1は2番目のビンの周波数域に含まれるようになり、結果としてS1のフーリエ変換結果のピークは2番目のビンに移ります。この段階で畳み込みを行うと元々f0にあったS0のピークはf0より1つ前と1つ後の2つのビンに分かれ、ツインピークが現れるようになります。本文書は教育目的ではありませんので、数学的な説明はこれで終了しますが、畳み込みについては(4-2-6)にも記述しています。
補足4 S1のトレンド除去により付加される直線成分のPSDの悪影響に対するS1とSRの周波数の関係
(4-1-3)のS1が振幅Gの三角関数でその周波数がk番目のビンの周波数と同じで、SRは(4-1-3)で使用したような複雑なものではなく振幅Aの単なる三角関数でその周波数はm番目のビンの周波数と同じとします。そうするとトレンド除去により付加されたS1の直線成分によるm番目のビンにおけるPSDとSRのPSDの比は式(17)及び式(14)により
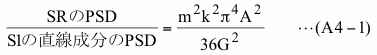
となります。なお、SRの周波数はm番目のビンの周波数と同じと仮定していますので、他のビンでは上の比は0.0となります。SRのPSDがS1に付加された直線成分によるPSDによって見にくくなる状態は上の比が1.0以下になるとすると、そのような状態になるS1の振幅とSRの振幅の比は
![]()
となります。この式によりS1及びSRの周波数が両方とも低いと(m及びkの値がともに小さくなる)振幅が相当大きなSRでも見にくくなりますが、どちらかの周波数が高ければS1に付加された直線成分による影響は小さくなります。
ここで、図4-10の例ではkは8になりますので、これを上式に代入すると、SRのPSDとS1のトレンド除去により付加された直線成分によるPSDが同じ値になるA/Gの値は0.076/mとなります。これはS1の振幅を1.0としてmを1番目のビンとするとSRの振幅が0.076、mを100番目のビンとするとSRの振幅が0.00076であればSRのPSDとS1のトレンド除去により付加された直線成分によるPSDが同じ値になるということです。mが100番目のビンの場合はまだ良いかもしれませんが、mが1番目のビンだとSRが少々大きくてもS1に付加された直線成分の影響でSRのPSDが見にくくなってしまいます。なお、図4-10で使用したデータの場合はmが20万番目程度であればSRのPSDとS1のトレンド除去により付加された直線成分によるPSDが同程度の値になりますが、実際のmの最大は4000ですので図4-10(d)ではSRはまったく視認できません。
これに対し、図4-12の例ではkは1600で、SRのPSDとS1のトレンド除去により付加された直線成分によるPSDが同じ値になるA/Gの値は0.00038/mとなります。この場合はmが百数十番目程度(周波数では100程度)より大きければSRのPSDがS1のトレンド除去により付加された直線成分によるPSDと同程度あるいはそれ以上になります。実際、図4-12(d)では図の中央よりやや右側あたりからSRの存在がわかるようになっています。
前ページは左矢印をクリックしてください