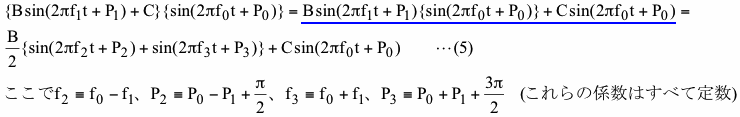お問合せは
->こちらへ<-

パワースペクトル密度計算 (スペクトル解析)
小額定型計算 PD001A/B
小額定型計算業務はお取り扱いするデータの形式、計算内容、計算結果の内容及び形式やデータ授受方法といった業務全般を定型化することでコスト削減及び納期短縮を図った計算サービスです。科学、技術研究のみではなく、商業や工業のいろいろな分野のデータの解析にご利用下さい。小額定型計算業務については->こちら<-をクリック下さい。
図を含む本文書の著作権はCygnus Research Internationalに帰属します。無断転載はお断り致します。
PD001A/B ユーザーガイド 2/7
目次
(1章) PD001シリーズの要約
(1-1) PD001シリーズで行う計算について
(1-2) お客様がご指定できる計算設定項目の要約
(1-2-1) トレンド除去; 全てのケースで個別に指定
(1-2-2) PSDの値の信頼区間のパーセンテージ; 全ケースで同一の値を指定
(1-2-3) テューキー窓関数のテーパー比; ケースB1、B2及びB3のみ適用 値は個別に指定
(1-2-4) 周波数領域での平滑化(以下FDSと略)ビン巾; ケースA1、B1及びC1の3ケースを除く全ケースで個別に指定
(1-3) 計算手法
(1-4) 入力データ(お客様のデータ)について
(1-5) プロダクツ
(1-5-1) 結果ファイル
(1-5-2) PDF形式の図
(1-6) 料金、納期およびご発注手順
(1-7) 個人情報、お客様のデータに関する情報保護
(2章) プロダクツの詳細及びその使用例
(2-1) 結果ファイル(本業務で納入するファイル)
(2-1-1) 結果ファイルのフォーマット(形式)
(2-1-2) 結果ファイルに記述する計算結果の内容
(2-1-2-1) 周波数 (Frequency)
(2-1-2-2) 周期 (Period)
(2-1-2-3) PSD (PSD)
(2-1-2-4) PSDの信頼区間 (Conf Int)
(2-1-2-5) 分散のパーセンテージ (% of Var)
(2-1-2-6) 振幅 (Amplitude)
(2-1-2-7) 位相 (Phase)
(2-1-3) 結果ファイルに書き出された情報の利用方法及び使用例
(2-1-3-1) 結果ファイルの値を用いて独自の図を作成したい場合
(2-1-3-2) PSD及びPSDの信頼区間の使用方法
(2-1-3-3) 特定の周波数での変動の巾(大きさ)を知りたい場合
(ケース1) 信号は振幅が一定の単一の周波数の三角関数で表される場合
(ケース2) 信号は振幅が一定の異なった周波数の三角関数を足し合わせたもので表される場合
(ケース3) 信号は単一の周波数の三角関数だが、振幅が時間とともに変動する場合
(ケース3-1) 信号の振幅の変動そのものが三角関数の形の場合
(例1) 信号は三角関数で周波数はf0。信号の振幅は周波数f1の三角関数の形で変動
(例2) 信号は三角関数で周波数はf0。信号の振幅は定数に周波数f1の三角関数を足し合わせた形で変動
(ケース3-2) 信号の振幅の変動そのものは三角関数ではない場合
(ケース4) 信号は周期的だが、三角関数の形ではない場合
(2-1-3-4) 特定の周波数域内の変動が全体の変動と比べてどの程度強いのかを知りたい場合
(2-1-3-5) 簡易デジタルフィルター(PD001Aのみ適用)
(2-1-3-6)データ中の値の変動の振幅を求める他の方法
(2-2)図
(3章) PD001シリーズ用のデータファイルの作成手順例
(4章) 各種指定項目の設定について
(4-1) トレンド除去;有無 無指定時は有
(4-1-1) トレンドとは? 除去の目的は?
(4-1-2) トレンド除去の例
(4-1-3) トレンド除去で問題が発生する例
(4-2) テューキー窓関数のテーパー比;%で表したテーパー比 無指定時は10%
(4-2-1) 窓関数を適用する理由
(4-2-2) 窓関数の適用とは
(4-2-3) ハニング窓関数;使用すると問題が生じる場合について
(4-2-4) 本小額定型計算業務 PD001Aでハニング窓関数を適用したPSDのみではなく、窓関数非適用及びテューキー窓関数を適用したPSDも計算する理由
(4-2-5) ハニング窓関数によるデータ両端近くの減衰を少なくする方法
(4-2-6) 窓関数が持つFDSに似た効果について
(4-2-7) IFDSは必ずしもPSDを平滑化しない
(4-2-8) 窓関数適用によるPSDや振幅スペクトル減衰に対する補正
(4-2-9) 窓関数適用時の補正の効果
(4-2-10) テューキー窓関数のテーパー比がPSDに与える影響
(4-3) 周波数領域での平滑化(FDS)ビン巾; 1、3、5、7等奇数 無指定時は無し(1)、3及び7
(4-3-1) PSDに対するFDS
(4-3-2) 振幅スペクトルに対するFDS
(4-3-3) FDSを適用した場合の周波数解像度
(4-3-4) FDSに代わる他の平滑化法
補足1 コンピュータを用いて計算をする際に生じる誤差について
補足2 パワースペクトル密度関数のスペクトル漏れと窓関数の関係について
補足3 データ長が短いと単一のピークが現れ、長いとツインピークが現れる理由
補足4 S1のトレンド除去により付加される直線成分のPSDの悪影響に対するS1とSRの周波数の関係
(2-1-3-3) 特定の周波数での変動の巾(大きさ)を知りたい場合
この節およびそれ以後では興味のある変動を信号と呼び、それ以外はノイズと呼びます。また、この節以後では信号ビンということばを使用します。(2-1-2-1)で記述したようにビンというのはその中心周波数が結果ファイルに書き込まれた周波数で周波数幅はPSDの周波数間隔と等しい周波数領域のことですが、信号ビンはその周波数領域内に実際の信号が含まれるビンのことです。なお、信号ビンの中心周波数(結果ファイルに書き込まれた周波数)は必ずしも信号の周波数と一致するとは限りません。
この節ではデータには信号しか含まれていない場合の結果を示します。このようなデータは現実的ではないのですが、PSDの計算によって得られる振幅(式(3)のAm)が実際の信号の振幅に比べどのようになるのか、信号の波形によってどのように変わるのかといった点を明らかにするためには好都合ですので、あえてノイズのないデータを使用しています。データにノイズが含まれている場合については(2-1-3-5)で記述致します。なお、以下に信号の波形が異なる幾つかのケースについて説明致します。
(ケース1) 信号は振幅が一定の単一の周波数の三角関数で表される場合
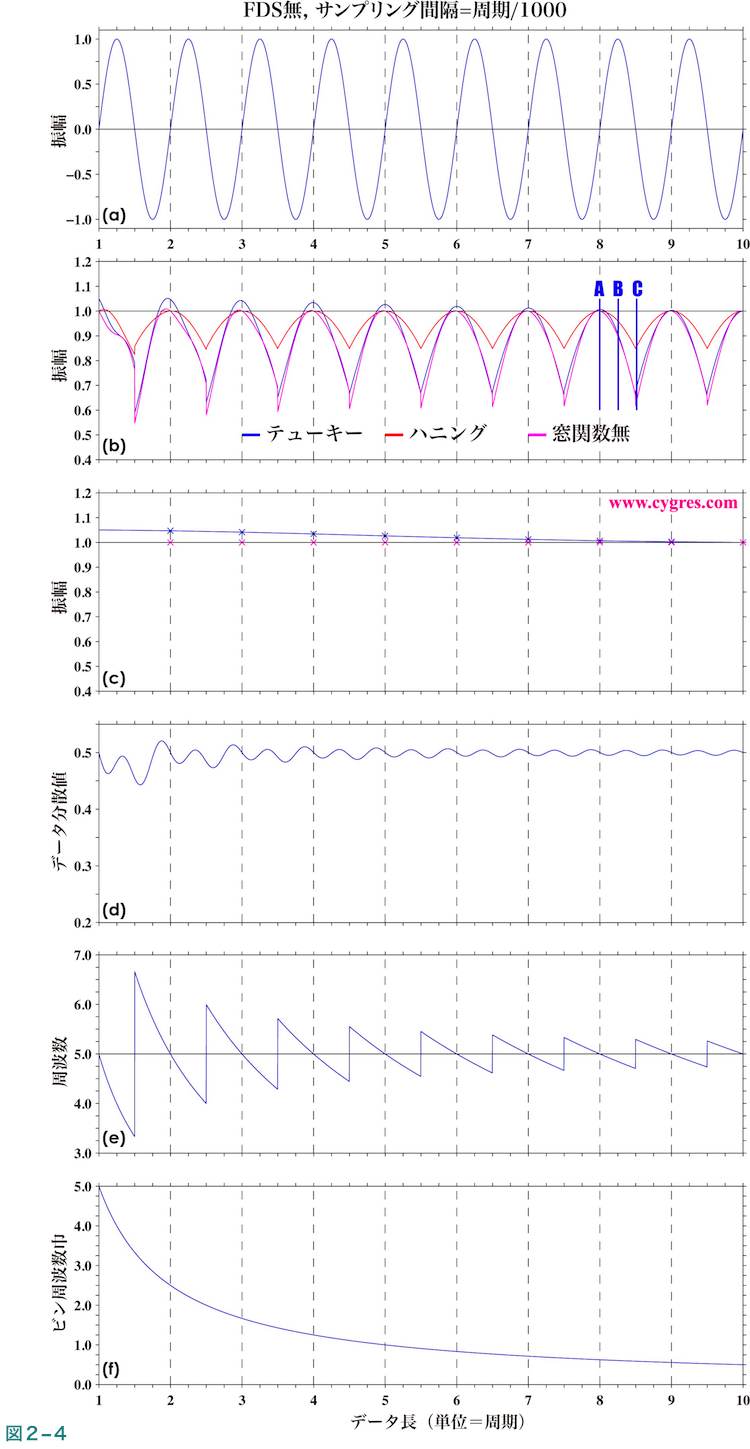
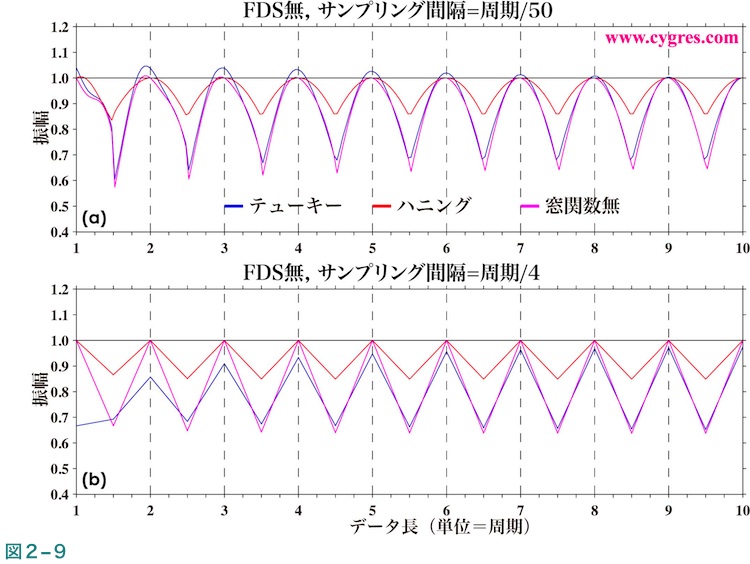
このケースは最も単純なケースで、図2-4(a)にこのケースのデータの時系列を示します。なお、上で記述したように、このデータには信号以外のものは含まれていません。この図の横軸(x軸)は時間ですが、単位は信号の周期を使用しています。実際にはデータは0.0から始まっているのですが、データ長が短い場合は計算結果の変動が大きいので1.0より短い部分は省略しています。なお、このデータのサンプリング間隔は信号の1周期の1/1000で、横軸1目盛(1周期)の間に1000個のデータがあります。
図2-4(b)は計算された信号ビンの振幅が、データが増えるにつれどのように変化するかを示します。図2-4(a)は横軸が単純に時間をあらわす普通の時系列図ですが、図2-4(b)およびそれより下の各図の横軸は個々の計算を行った際のデータの長さをあらわします。具体的には横軸の値が2.0の値は2000個のデータ使用した結果の値で、横軸の1.0の目盛りの間には500回の計算結果が含まれます(図全体では4501回x3窓関数、計13503回の計算結果を示します)。なお、この図を作成するための計算においては(4-1-3)に記述するような理由でトレンドの除去は行っていません。また、この図および以下に示す各図では縦軸の単位は明確にする必要が無い場合が多いので、無記入としています。
図2-4(b)中の黒の水平の実線は信号の実際の振幅(1.0)を示します。図中の青色の短い縦の実線で示したデータ長A、B及びCでのPSDや振幅スペクトルは後ほど示します。図中の縦の黒の破線(水平1.0間隔で計8本)は信号ビンの中心周波数が信号の実際の周波数に一致している場合のデータ長(本ケースではサンプリング間隔が固定されていますのでデータ長のみでPSDおよび振幅計算の周波数が決まります)の位置を示します。なお、このように信号ビンの中心周波数が信号の実際の周波数に一致している場合を以下では周波数一致と略します。
周波数一致を成立させるためには既存のデータではサンプリング間隔は変えられませんので、PSDを計算する時点でデータ数を調節します。具体的にはPSDの計算は(2-1-2-1)で記述したように1/(サンプリング間隔xデータ数)という周波数間隔で行われますが、信号の周波数がfである場合はf x (サンプリング間隔xデータ数)が整数になるようにデータの数を減らすか、あるいは値が0のデータを追加します。なお、値が0のデータを追加する処理をゼロパッディングと呼びます。例として信号の周波数が1.5サイクル/秒(1.5Hz)、データの個数が198でサンプリング間隔が0.5秒とします。このデータをすべて使うと1.5x(198x0.5)=148.5となり、この値は整数ではないのでどのビンの周波数も信号の周波数と一致しません。しかしデータを2個減らして196個にすると1.5x(196x0.5)=147なので周波数一致が成立します。また、2個ゼロパッディングを行いデータの個数を200個にすると1.5x(200x0.5)=150となり、この場合も周波数一致が成立します。
図2-4(c)は図2-4(b)と同様ですが周波数一致が成立している場合のみを抽出してプロットした図です。また、図2-4(d)はデータの分散がデータの長さによってどのように変化するかを示します。図2-4(e)は信号ビンの周波数を示す図で、図中の黒の実線は実際の信号の周波数を示します。図中で、縦の黒の破線と青の線(信号ビンの周波数)が交わる点は黒の実線(実際の信号の周波数)も交わっていることが分かりますが、これが周波数一致です。図2-4(f)はビンの周波数巾で周波数解像度と同じです。この値はPSDや振幅スペクトルのピークを信号の周波数と推定した場合に、推定した周波数と実際の信号の周波数との差の範囲を示します。これらの図により、データを増やすにつれビンの周波数巾は狭くなり周波数の推定値はより正確になることがわかります。ただし、データを増やすことによる信号の周波数推定の改善の効果はデータ数が少ない場合は大きいのですが、データ数が元々多い場合はあまり無いことがわかります。
ここで、図2-4(b)に戻ります。この図により信号ビンの振幅は周波数一致が成立した場合(縦の黒の破線の位置)は実際の信号の振幅にほぼ一致し、それ以外の場合は実際の信号の振幅より小さくなることがわかります。ここで、信号ビンの振幅を実際の信号の振幅の推定値とすると、このように周波数一致が成立しないと信号の振幅推定値は実際の値と一致しなくなるのですが、これはコンピュターで計算を行う場合に常に生じる計算の誤差ではありません。周波数一致が成立する場合は、(2-1-2-6)の式(3)の右辺中で信号ビンのAmの値は実際の信号の振幅と同じになり、他のAmの値は計算誤差の範囲内でゼロになります。しかし周波数一致が成立しない場合は本来の信号の周波数とは異なる周波数の変動にいわば無理矢理分解させることになりますが、その場合でも式(3)自体は成立しなければなりませんので、その結果スペクトル漏れという現象がおき、信号ビンのAmの値は実際の信号の振幅よりは一般的に小さくなり、それ以外のビンのAmの値はゼロよりは大きな値になってしまいます。なお、スペクトル漏れの原因のこのような解釈はPSDや振幅スペクトルを実際に計算する式の上からの解釈ですが、窓関数の概念を用いたスペクトル漏れの原因のより数学的な解釈は補足2に記述します。
この図ではデータ長が信号の周期の数倍より長ければ、それ以上データを増やしても計算結果は概ね同じパターンの繰り返しになっています。ここで前述したように、データ長が長くなるとビンの周波数巾は小さくなるのですが、周波数一致が成立しない場合の信号ビンの振幅、すなわち振幅推定値と実際の信号の振幅の差はほとんど変わりません。これは別の見方をすれば、データ数が多い場合は少ない場合に比べ、同程度に精確な振幅推定値を得るためには信号ビンと実際の信号の周波数差をより小さくしなければならないということになります。PSDの場合はデータ長が十分に長い場合は(4-3-1)に記述するように周波数解像度を犠牲にしてFDSを適用することによってより精確な推定値を得ることができますが、振幅スペクトルの場合は後述((4-3-2)で詳細に記述)するようにFDSがうまく機能しません。なお、(2-1-3-5)で示すようにデータにノイズが含まれている場合は図2-4で示す程度のデータ長では計算結果が安定した繰り返しにならないこともあります。
なお、振幅スペクトルで最大の値を示すビンは大抵は信号ビンになるのですが、稀に信号ビンの隣のビンが最大になる場合もあります。そのような状況はデータ長Cのように信号の周波数が信号ビンの周波数範囲の上限または下限に近い場合、すなわち2つのビンの中心周波数の中間付近にある場合に発生します。具体的にはこの図で示す4501回の計算のうちテューキー窓関数を使用した場合は84回、ハニング窓関数を使用した場合は19回、窓関数を使用しなかった場合は136回発生しています。ここで示すケースでは実際の信号の周波数がわかっていますので、信号ビンはその周波数から決められますが、実際のデータではPSDや振幅スペクトルよりピークを探し出して信号ビンを決めることになりますので、場合によれば若干の注意が必要となります。なお、この件については補足2でその原因を記述します。
窓関数については、図2-4(b)及び図2-4(c)ではハニング窓関数を適用した結果が最善となっています。具体的にはデータ長が8.0から9.0の間では信号ビンの振幅と実際の信号の振幅との差の最大値は窓関数を適用しなかった場合(窓関数無し)は0.38、テューキー窓関数を適用した場合は0.34、ハニング窓関数を適用した場合は0.15と、周波数一致が成立しない場合の信号ビンの振幅と実際の信号の振幅との差はハニング窓関数を適用した場合が最も小さくなっています。ただし、ハニング窓関数を適用するとデータは中央部以外はかなり減衰させられますので、(4-2-3)で記述するように場合によれば問題が生じることがあります。ここで示したデータの場合はデータのどの部分をとっても同じような変動しかありませんので、中央部以外を減衰させても特に問題が生じるようなことはなく、ハニング窓関数のメリットが最大限に生かされると同時に信号によるピークの巾がやや広くなる(後述致します)ということ以外のデメリットは目立たないという結果になっています。
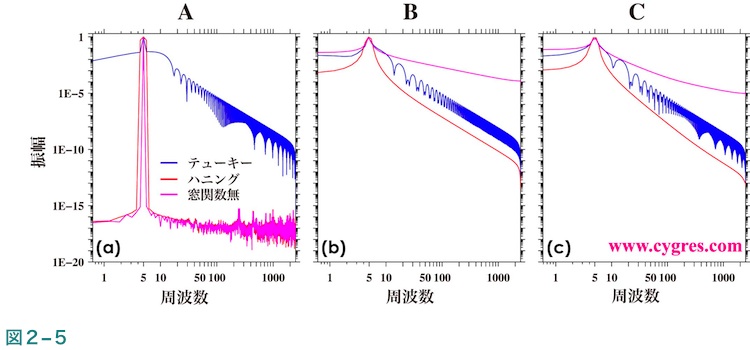
次に振幅スペクトルですが、図2-4(b)で青色の短い縦の実線で示したデータ長がA、B及びCの場合の周波数ゼロを除く全周波数域の振幅スペクトルを図2-5の左から順に示します。ここで、データ長Aは周波数一致が成立している場合で、データ長Cは信号ビンの周波数が実際の信号の周波数から最も離れている場合です。データ長Bはデータ長AとCの中間に相当する長さということで選択しています。
この図では縦軸、横軸ともに対数スケールを採用しています。対数スケールのメリットは広範囲の値を表示できることですが、結果として見た目では小さな値の部分が拡大される反面、大きな値の部分が縮小されることになります。なお、周波数ゼロの値(結果ファイルでは2行目のビン)を除いた理由は、周波数ゼロの成分というのはデータの平均値に該当するもので、データの値の変動には一切寄与せず通常はPSDの計算時には除去するからで、この文書でも周波数ゼロのビンは例外を除き無視しています。なお、ゼロの対数値はマイナスの無限大で図2-5のような対数スケールの図には周波数ゼロの値は示すことができません。
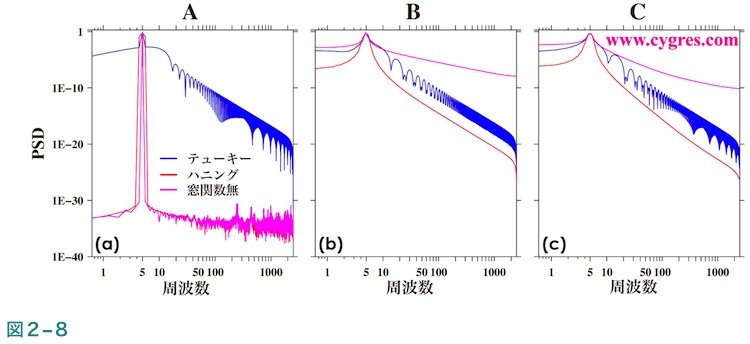
図2-5(a)は周波数一致が成立している場合ですが、窓関数を適用しなかった場合(紫線)及びハニング窓関数を適用した場合(赤線)は信号の周波数(5.0)ではっきりとしたピークが現れ、ピーク以外の周波数での値は非常に小さな値になっています。理論的には窓関数を適用しなかった場合は信号ビン以外の値、ハニング窓関数を適用した場合は信号ビンおよびその両隣のビン以外はゼロでなければなりませんが、実際の計算値はゼロにはなりません。これは補足1に記述するようにコンピュータで計算を行えばほとんど常に生じる計算誤差によるものです。
図2-5(a)ではテューキー窓関数を使用した場合(青線)は多数の小さな丘のようなものが周波数全域に見られます。この図を見るとテューキー窓関数の使用に関し危惧の念が生じるのですが、いろいろな信号やノイズが含まれている現実のデータのPSDを計算するとこのような丘状のものが出てくることは実際にはほとんどありません。ハニング窓関数でももし一定の周波数間隔ではなく連続したスペクトルを計算するとこのような丘状のものが補足2に示すように出てきます。この丘状のものが生じる原因は窓関数がFDSに似た効果(以下ではIFDSと略します)を持つためですが、その詳細も含め、窓関数については(4-2)に記述します。周波数一致が成立しない場合は前述したようにスペクトル漏れが生じますが、主にそのために図2-5(b)及び(c)で見られるように信号ビン以外のビンの振幅もかなり大きくなります。これらの図により、最もスペクトル漏れの悪影響が少ないのはハニング窓関数を適用した場合(赤線)で、テューキー窓関数を適用した場合(青線)がそれに続き、窓関数非適用の場合(紫線)が最悪となることがわかります。
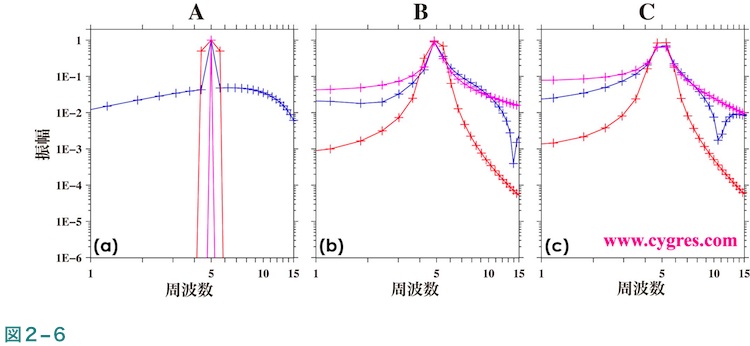
図2-6は信号ビンの周辺のみを拡大して表示した図で、図中のプラス記号(+)はビンの周波数及び値を示します。周波数一致が成立する場合(図2-6(a))は信号のピークは窓関数非適用(紫線)とテューキー窓関数(青線)を使用した結果では1点の鋭いものになりますが、ハニング窓関数(赤線)を適用すると信号のピークは頂上付近が3点のやや巾が広いものになります。ハニング窓関数を適用した場合にピークの巾が広がる理由については(4-2-6)に記述します。周波数一致が成立しない場合(図2-6(b)及び(c))は主にスペクトル漏れのために信号によるピークがあまりはっきりしなくなりますが、縦軸のスケールをこれらの図のように対数スケールではなく一般的な均等スケールにするともう少しはっきりします。
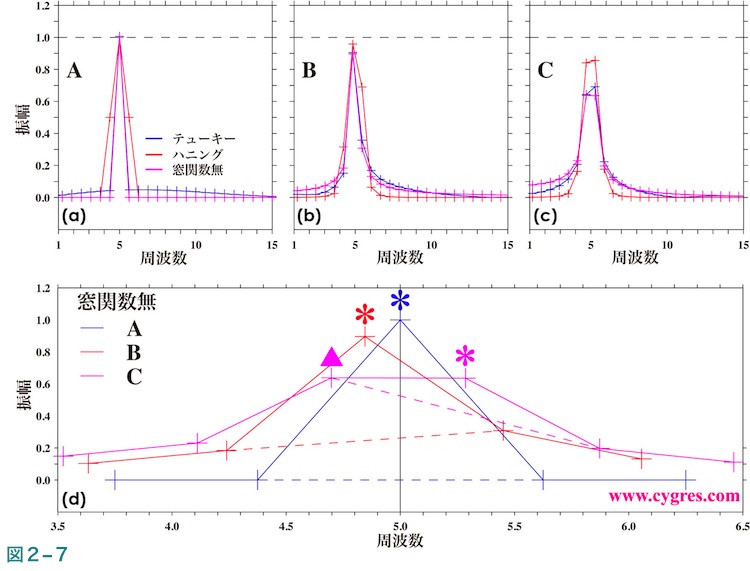
図2-7(a)、(b)及び(c)は図2-6(a)、(b)及び(c)と同じなのですが、値を読み取りやすくするために縦軸及び横軸双方とも均等スケールにした図で、これらの図中の水平の黒の破線は信号の実際の振幅(1.0)です。これらの図により計算された振幅がどの程度実際の信号の振幅に近いか(推定がどの程度精確か)がわかります。
図2-7(d)はデータ長がA(青線)、B(赤線)及びC(紫線)の3ケースで窓関数非適用の場合の信号ビン周辺の振幅スペクトルの詳細を示します。この図の中央にある縦の黒の実線は信号の実際の周波数の位置で、色のついた米記号(*)は信号ビンを示します。なお、信号ビンの両隣のビンの値の間に色のついた破線を描画しています。この図より周波数一致が成立する場合(A;青線)は信号ビンの値はほぼ信号の実際の振幅に一致し、それ以外のビンの値は実質ゼロで信号によるピークは非常にはっきりした左右対称のもの(横軸を対数スケールにすると見た目では非対称になります)になります。しかし、信号ビンの周波数が信号の実際の周波数と一致しなくなると信号ビンの両隣のビンの値間の差が次第に大きくなり(色付き破線の傾きが大きくなり)ピークの形は次第に左右非対称になります。そして、データ長C(紫線)の場合のように実際の信号の周波数が信号ビンの周波数域の下限に近くなると信号によるピークは頂点がほぼ平坦な2点のピークになってしまいます。なお、この図ではわかりにくいのですが、このケースでは前述したように信号ビン(米記号;値は約0.636)より信号ビンより低い周波数のビン(三角記号;値は約0.638)の値の方が大きな値になっています。この差は約0.002と、あまり大きくはないのですが、補足1に記述するような計算上の誤差で生じたと解釈できるほど小さくはありません。また、この計算結果はノイズをまったく含まないデータによるものですので、統計的な誤差でもありません。このようなケースは実際の信号の周波数が米記号のビンと三角記号のビンの中心周波数のちょうど中間付近にある場合なので、信号の周波数をそのように捉える場合はいいのですが、どちらかのビンの中心周波数を信号の周波数とする場合は注意が必要になります。
図2-7より横軸(周波数軸)を均等スケールにした振幅スペクトル上で見られるピークが左右非対称な場合は実際の信号は最大値を示すビンの中心周波数ではなくそれより裾野(ピークのビンに隣接するビン)が高いほうに存在することがわかります。ただし、ピークの形が頂上が平坦な2点のピークの場合はその2点間の中間付近にあり、どちらに近いかは振幅の値だけでは判断できません。もっとも実際のデータの振幅スペクトルではいろいろなノイズや他の信号が含まれているのが普通ですので、これほど単純には判定できないと思われます。
ここで、参考のために図2-5に対応するPSDを図2-8に示します。
図2-9(a)は図2-4(b)と同様に信号ビンの振幅を示しますが、サンプリング間隔を100倍、すなわちデータの数を1/100にした結果です。図2-9(a)と図2-4(b)を比較しても見た目でわかるほどの違いはありません。図2-9(b)はサンプリング間隔をさらに長くし、図の横軸1目盛りの間に4点のデータしかないようにした結果ですが、計算を行った点がはっきりとわかるようになった以外は、例えば計算された振幅と実際の信号の振幅の差が目立つというような違いはありません。これらの図だけから判断すると、データ数が比較的少数でもかなり精確な結果が得られるということになりますが、ここで使用したデータは目的とした信号以外は一切含まれないもので、いろいろな信号やノイズが含まれているような現実的なデータでは一般的にはデータ数が多い方が有利となります。なお、前述したようにデータの数やサンプリング間隔はPSDが計算できる周波数間隔や最高の周波数に影響しますので、サンプリング間隔をあまり長くしたりデータの数をあまり少なくしたりすると、目的に合わない結果しか得られない可能性もありますので、注意が必要です。
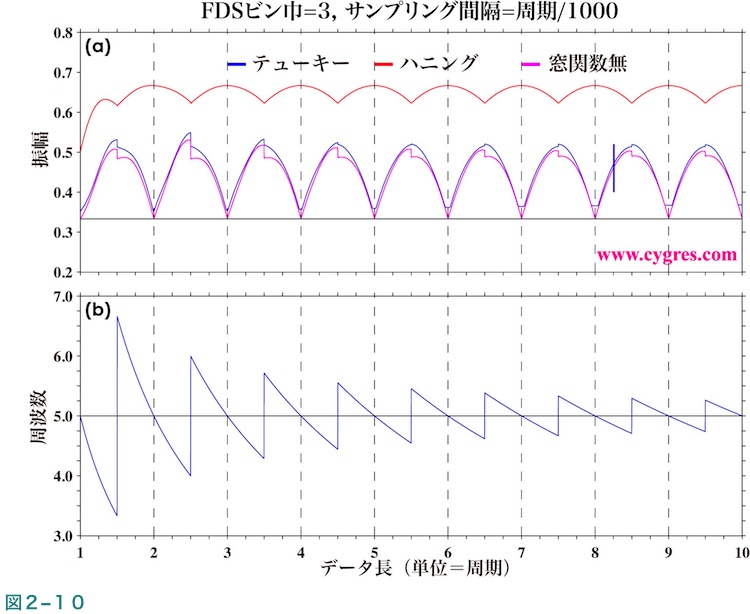
FDS(周波数領域で行う平滑化)はPSDを計算した後に、その値を滑らかにするために行う単純な重みなしの移動平均で、例えば平滑化巾3ビンのFDSの場合はFDS適用前のk-1番目、k番目及びk+1番目のPSDの値をそれぞれP(k-1)、P(k)及びP(k+1)とすると、FDS適用後のk番目のビンの値は{P(k-1)+P(k)+P(k+1)}/3となります。ここで、”重みなし”という意味はこの平均を計算する際にP(k-1)、P(k)及びP(k+1)のどの値にも同じ係数、1/3が掛けられていて、これらの値はすべて対等に扱われていることをさします。これに対し、例えば{P(k-1)+2P(k)+P(k+1)}/4のようにして計算すると、P(k)に掛けられる係数はP(k-1)やP(k+1)に掛けられる係数の2倍になっていますのでP(k)をP(k-1)やP(k+1)に対し重視したことになり、このような場合は”重み付き”の移動平均と表現します。
FDSはPSDに対しては有効なのですが、振幅に対しては有効ではありません。平滑化巾3ビンのFDSを適用した場合の信号ビンの振幅を図2-4(b)と同様の様式で図2-10に示します。信号ビンをkとした場合はP(k-1)=P(k+1)=0及びP(k)=1.0ですので、上の式によりFDS適用後の真の振幅スペクトルの値は図中の水平の黒の実線で示すように実際の信号の振幅の1/3になりますが、実際の計算結果はかなり大きくなってしまいます。このように振幅にFDSを適用すると無意味な結果になりますので、PD001シリーズの結果ファイルにはFDSを適用した場合は振幅は書き出さないようにしています。なお、この件については(4-3-2)により詳細に記述しています。
(ケース2) 信号は振幅が一定の異なった周波数の三角関数を足し合わせたもので表される場合
この場合は式(3)に従いデータの変動は複数の周波数の信号に分解されることになります。このケースの例は省略致します。
(ケース3) 信号は単一の周波数の三角関数だが、振幅が時間とともに変動する場合
(2-1-2-6)の式(3)でAmは時間によらない定数と記述しましたが、このケースは信号がそれでは表現できない場合です。以下で複数のケースに分けて記述致します。
(ケース3-1) 信号の振幅の変動そのものが三角関数の形の場合
(例1) 信号は三角関数で周波数はf0。信号の振幅は周波数f1の三角関数の形で変動
結論から先に述べますと、データが十分に長い場合はPSD及び振幅スペクトルともにf0とf1のどちらの周波数にもピークは現れず、f0-f1(f0のほうがf1より小さい場合はf1-f0)とf0+f1の2つの周波数に同じ大きさのピークが現れます。なお、以下ではf0のほうがf1より大であるとします。
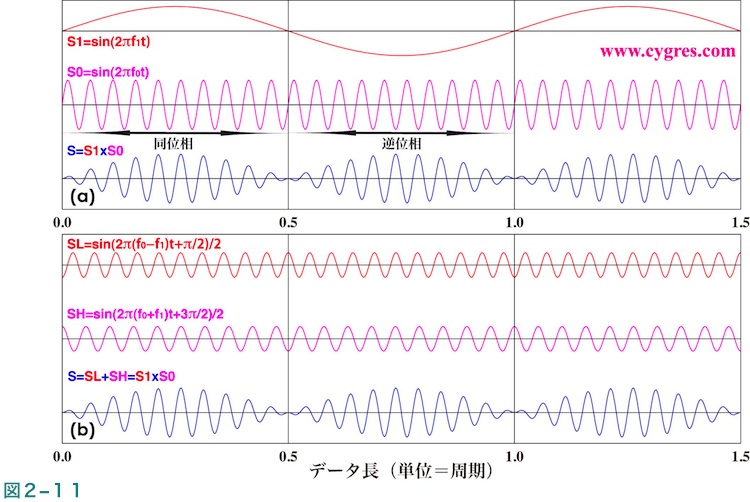
このケースのデータの時系列図を図2-11(a)に示します。この図の一番下のSはここで使用するデータで、これは図中央の信号S0に一番上の振幅変動S1を掛けたものになっています。この図では横軸目盛で0.0から0.5の間はSの”山”の位置とS0の”山”の位置が一致(同位相)していますが、横軸目盛が0.5から1.0の間はSの”山”の位置とS0の”谷”の位置が一致(逆位相)しています。これはS1の値が横軸目盛0.0から0.5の間は正で横軸目盛0.5から1.0の間は負のためですが、いずれにしろ周波数f0の信号が常に存在しているように見えますし、実際に存在しています。
この式中のBは定数で図2-11中では1.0になっています。式(4)によりこのケースのデータは振幅がともにB/2で周波数がf0-f1(=f2;SL 低周波数側信号)及びf0+f1(=f3;SH 高周波数側信号)の2つの信号の和として表されることがわかります。ここで重要な点はこの2つの信号の振幅は定数であるということです。これは式(3)のAmが定数であることという条件と合致するためにこのデータのPSDを計算するとf0-f1とf0+f1にピークが現れるという結果になります。図2-11(b)の一番上の図はSL、中央の図はSH、一番下の図はSLとSHを足し合わせた結果を示します。この図ではSLとSHは全く同じように見えますが、両者の”山”の数を数えると両者が異なる周波数の変動であることがわかります。図2-11(b)の一番下の図は図2-11(a)の一番下の図と同じになります。なお、式(4)の青の下線を引いた部分より、f0とP0をf1とP1に交換しても全く同じ結果になることがわかります。
では次にデータがどの程度長ければこのようにf0-f1とf0+f1にピーク(この2つをあわせたものを以下ではツインピークと称します)があらわれるのかという問題に移ります。実際の計算結果は後で示しますが、図2-11に示すようなデータがあったとして、データ長(サンプリング間隔xデータ数)を少しずつ長くしながらPSDを計算すると、最初はf0にしかピークがないものになります。このような状態はデータ長がS1の周期の半分(図2-11の横軸で0.5)になるまで続きます。S1の周期の半分の点ではこのデータは信号S0にコサイン窓関数という窓関数を適用したものと同等になります。データ長をさらに長くしていくと、ツインピークが時々現れるようになり、その頻度が増えていきます。ただし、ここで現れる2つのピークの高さは必ずしも同じにはなりません。なお、データ長が短いとビンの周波数巾が大きくなりますので、最初の間はf0-f1とf0+f1は常に同じビンの中に入るためにツインピークは現れません。データ長がS1の1周期の長さになると正確な同じ高さをもったツインピークが現れます。それ以上データ長を長くしていくと概ねツインピークが現れますが、まれに単一のピークになることもあります。ただし、f0-f1とf0+f1両方について周波数一致が成立しない場合は2つのピークの高さは一致しませんし、形状も一般には異なります。一般的にはデータ長がS1の数周期以上になれば常にツインピークが現れるようになります。なお、このようにデータ長が短いと単一のピークが現れ、データ長が長いとツインピークが現れることの数学的な説明は補足3に記述します。
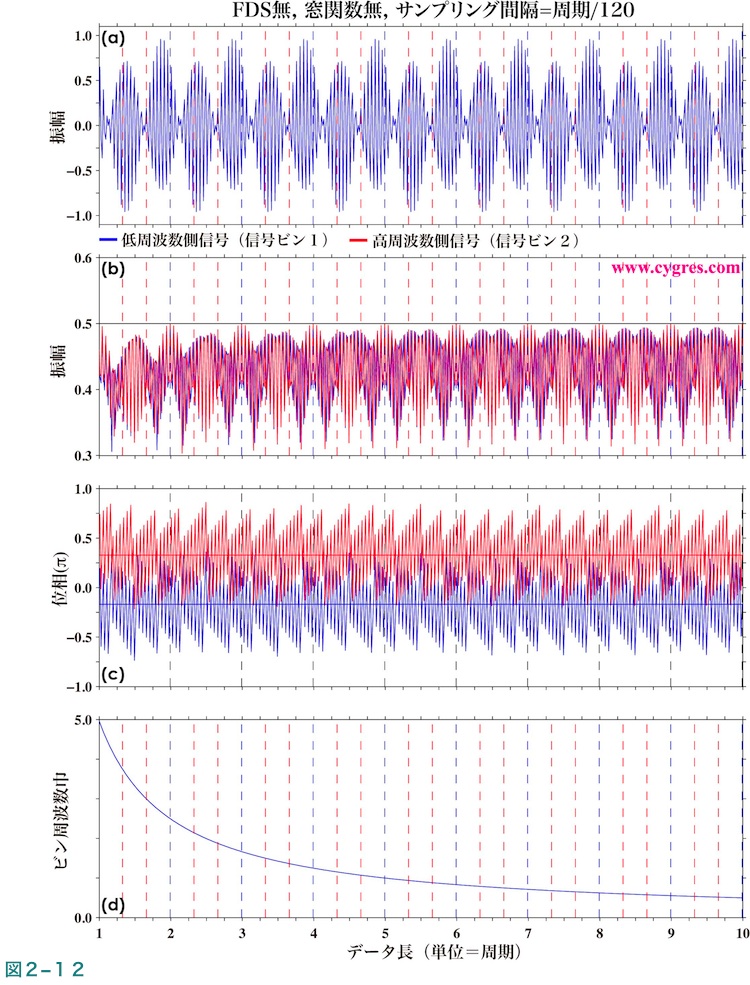
図2-12(a)にここで使用するデータの時系列を示します。この図は図2-11のSとかなり異なって見えますが、これは図2-12(a)のデータのP0及びP1(位相;式(4))の値はどちらもゼロではないからです。図2-12の一番下の図に表示した横軸の単位はS1の周期です。データ長が1.0より短い場合の結果は複雑なのでここでは割愛しています。以下ではf0-f1(低周波数側)の周波数を含むビンを信号ビン1、f0+f1(高周波数側)の周波数を含むビンを信号ビン2と称します。図中の青色の縦の破線は信号ビン1で周波数一致が成立しているデータ長、赤色の縦の破線は信号ビン2で周波数一致が成立しているデータ長を示します。ただし、この計算では信号ビン2で周波数一致が成立する場合は信号ビン1でも周波数一致が成立するように信号ビンの周波数を選択していますので、赤色の破線が引かれているデータ長では実際は両信号で周波数一致が成立しています。
図2-12(b)は計算された信号ビン1(青線)及び信号ビン2(赤線)の振幅がデータが増えるにつれどのように変化するかを示す図で、図2-4(b)と同様の図です。図中の黒の水平の実線は両信号の実際の振幅(0.5)を示します。この図は図2-4(b)と比べるとかなり見にくいので、部分的に拡大した図を後で示しますが、この図よりデータ長がS1の周期の数倍より長ければ、それ以上データを増やしても計算結果は概ね同じパターンの繰り返しになっていることがわかります。なお、この図を作成するための計算においては(4-1-3)に記述するような理由で図2-4の場合と同様にトレンドの除去は行っていません。
図2-12(c)は両信号ビンの位相を示す図で単位は度やラジアンそのものではなく1パイ分のラジアンで、最大は+1.0、最小は-1.0になります(円周率(パイ)ラジアンは180度に相当します)。図中の水平の青色の実線は信号ビン1の実際の位相を、赤色の実線は信号ビン2の実際の位相をそれぞれ示します。この図についても部分的に拡大した図を後で示します。図2-12(d)はビンの周波数巾で周波数解像度と同じで、これについては信号ビン1と2の間に違いはありません。なお、図2-12(b)〜(c)では窓関数を適用した場合の結果は図がさらに見にくくなるので割愛しています。
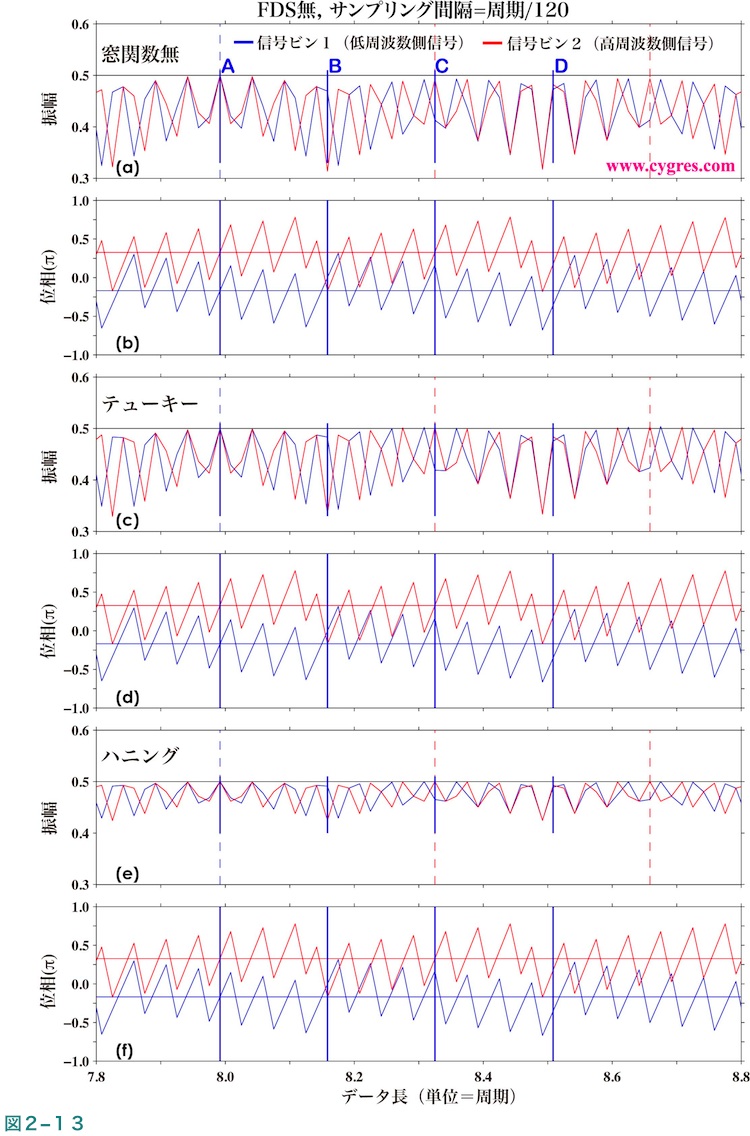
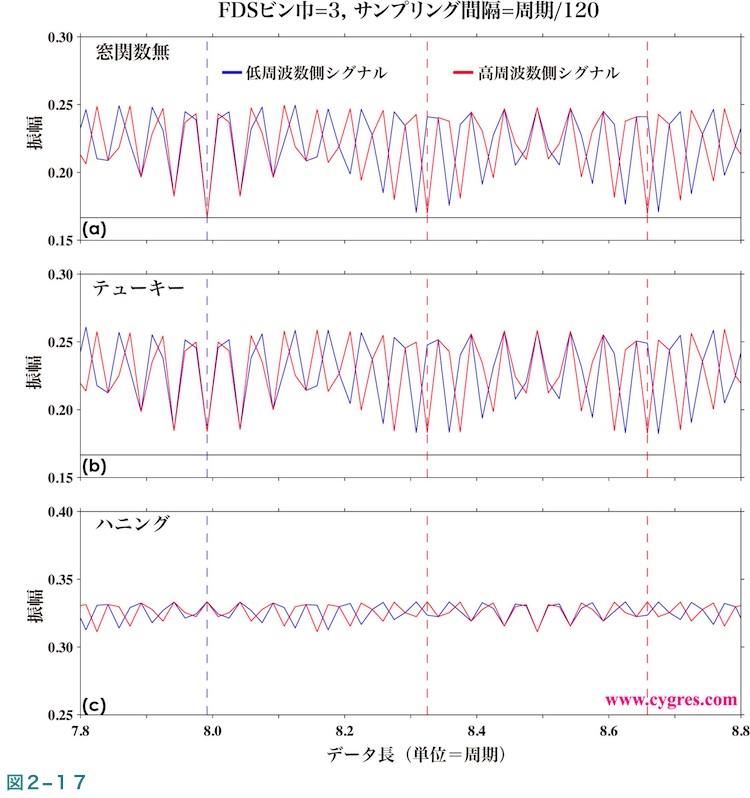
図2-13は信号ビンの振幅及び位相についてデータ長7.8から8.8迄の間のみ取り出し水平方向に拡大した図で、図中の縦の破線や横の実線の意味は図2-12と同じです。この図では図2-12と異なり、窓関数非適用の場合だけではなくテューキー窓関数やハニング窓関数を適用した場合の結果も示しています。この図により、精確な振幅および位相の値を得るためにはSL(信号ビン1に該当)やSH(信号ビン2に該当)について周波数一致を成立させることが重要であることがわかります。なお、図2-4(b)と比較すると図2-13(b)の信号ビンの振幅がかなり激しく変動しているように見えますが、これはSLやSHの周期はこの図で水平軸の単位に使用しているS1の周期に比べかなり短いためで、もし水平軸の単位をSLとSHの平均の周期(S0の周期になります)に代え、それに応じてさらに水平軸を拡大すれば図2-4(b)のように緩やかに変動する図になります。
信号ビン1及び2とも周波数一致が成立しているデータ長を図2-13(a)中の青色の縦の実線Aで示しますが、この場合は各信号ビンの振幅及び位相双方とも実際の値とほぼ一致します。
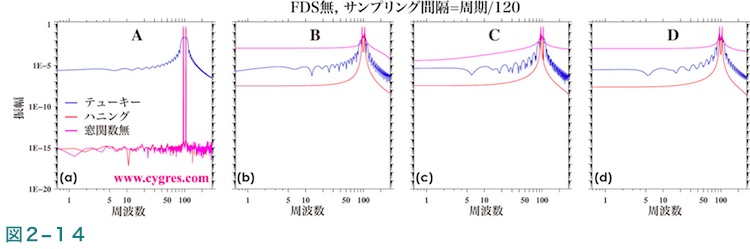
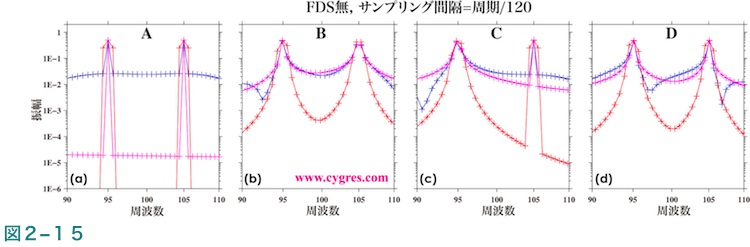
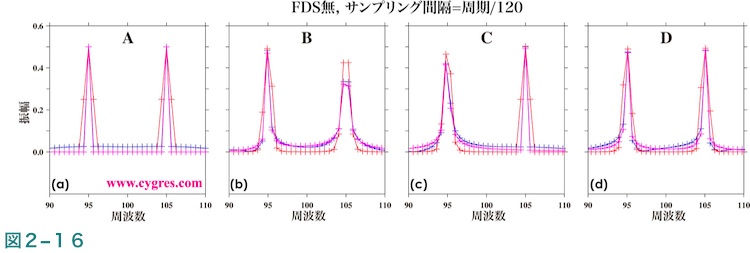
図2-14(a)にデータ長がA(図2-13(a)縦の青実線)の場合の全周波数領域の振幅スペクトルを示しますが、この図ではツインピークがはっきりとあらわれています。図2-15(a)はツインピーク周辺のみを取り出して拡大した図ですが、その様子がさらにはっきりとわかります。なお、この図中のプラス記号(+)はビンのある点です。テューキー窓関数を適用した場合は信号ビン以外のビンの振幅も比較的大きく、ハニング窓関数を適用した場合はピークは各信号ビンの両隣のビンも含めた3点のピークになりますが、これらは図2-5及び図2-6と同様です。図2-16(a)は対数スケールではなく均等スケールを使用した点以外は図2-15(a)と同じですが、この図より信号ビンの振幅はほぼ実際の信号の振幅(0.5)に一致すること及び、信号ビン以外のビンの振幅は図2-15で受ける印象ほど大きくはないことがわかります。
データ長がCの場合は信号ビン2のみで周波数一致が成立していますが、この場合は図2-15(c)及び図2-16(c)より信号ビン2のある高周波数側(右側)のピークは鋭いピークで、ピークの頂上の値は実際の信号の値(0.5)にほぼ一致しますが、信号ビン1のある低周波数側(左側)のピークは巾が広く、またピークの頂上の値は実際の信号の値より小さくなっています。データ長Bはデータ長AとCのほぼ中間で信号ビン1及び2とも周波数一致は成立していませんが、信号ビン1の周波数は実際の信号の周波数に近い場合です。この場合は図2-16(b)より信号ビン1(低周波数側)の値は実際の信号の振幅にかなり近い値になっていることがわかります。データ長Dの場合は各信号ビンの周波数と実際のそれぞれの信号の周波数との差はほぼ同じになっていますが、この場合は図2-16(d)より低周波数側のピークも高周波数側のピークも巾がデータ長Aの場合に比べやや広くなっていることがわかります。
下に平滑化巾3ビンのFDSを適用した振幅の一部を拡大した図を示しますが、この図のように振幅スペクトルにFDSを適用すると図2-10と同様にあまり意味のない結果しか得られません。
なお、各ビンの周波数からf0を引いた周波数でPSDの図を作成するとS1そのものの両側PSDの図が得られます。ただし、これは両側PSDですので元の周波数がf0より低い部分の周波数は負になります。この図は水平軸に書かれる周波数の値以外は元々のPSDの図と見かけ上は一緒となります。
(例2) 信号は三角関数で周波数はf0。信号の振幅は定数に周波数f1の三角関数を足し合わせた形で変動
この場合の信号を数式で表すと以下のようになります。
この式で振幅(B及びC)、周波数(f0及びf1)及び位相(P0及びP1)はすべて定数です。式(5)で青色の下線を引いた部分は式(4)の右辺に振幅C周波数f0及び位相P0の三角関数の変動を足し合わせたものになります。したがって、この信号の理論的なPSDは振幅がCで周波数f0のピークを中心として、f0からf1だけ高低両側に離れた周波数に対になった振幅B/2のピーク、計3つのピークを持つことになります。このケースはAM放送で使用される電波と似ています。AM放送で使用される電波の形式は周波数が一定の搬送波と呼ばれる電波の振幅を音声によって変化(変調)させたものですが、上の式ではf0が搬送波の周波数になり、f1が音声部分の周波数になります。もし式(5)がAM放送波を表すのであればラジオのダイアルをf0にあわせれば周波数f1の単調なトーンが聞こえることになります。なお、この例は例1の延長と考えられますので、詳細については割愛します。
(ケース3-2) 信号の振幅の変動そのものは三角関数ではない場合
この場合は信号の振幅D(t)の変動そのものも式(3)のようにいろいろな周波数の三角関数を足し合わせたものと考えます。そうしますと、信号は以下のような形で表現できます。
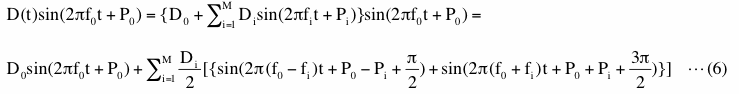
この式の右辺ではすべての係数は定数です。この式よりこの信号の理論的なPSDは周波数f0のピークを中心としてf0の高低両側にM個の対になったピーク、計1+2M個のピークを持つことになります。なお、前述したように各ビンの周波数からf0を引いた周波数でPSDの図を作成すると式(6)の左辺のD(t)そのものの両側PSDが得られます。これは式(6)がAM放送の信号を表すとすると、AM放送で送信される音声そのものの両側PSDが得られるということになります。このケースにノイズを加えた例を(2-1-3-5)に示します。
(ケース4) 信号は周期的だが、三角関数の形ではない場合
この場合でも信号は式(3)のように三角関数の和の形に分解されます。この->ページの図2<-で具体例をいくつか記述していますが、通常は複数のピークが現れ、信号の繰り返しの周波数は最も低い周波数のピークの周波数と一致します。なお、該当ページの計算はすべての例で窓関数は非適用で平滑化巾3ビンのFDSを適用しています。またすべての例で周波数一致が成立していています。
前ページは左矢印を、次ページは右矢印をクリックしてください