お問合せは
->こちらへ<-
パワースペクトル密度計算 （スペクトル解析）
小額定型計算 PD001A/B
小額定型計算業務はお取り扱いするデータの形式、計算内容、計算結果の内容及び形式やデータ授受方法といった業務全般を定型化することでコスト削減及び納期短縮を図った計算サービスです。科学、技術研究のみではなく、商業や工業のいろいろな分野のデータの解析にご利用下さい。小額定型計算業務については->こちら<-をクリック下さい。
図を含む本文書の著作権はCygnus Research Internationalに帰属します。無断転載はお断り致します。
PD001A/B ユーザーガイド 4/7
目次
(1章) PD001シリーズの要約
(1-1) PD001シリーズで行う計算について
(1-2) お客様がご指定できる計算設定項目の要約
(1-2-1) トレンド除去； 全てのケースで個別に指定
(1-2-2) PSDの値の信頼区間のパーセンテージ； 全ケースで同一の値を指定
(1-2-3) テューキー窓関数のテーパー比； ケースB1、B2及びB3のみ適用 値は個別に指定
(1-2-4) 周波数領域での平滑化（以下FDSと略）ビン巾； ケースA1、B1及びC1の３ケースを除く全ケースで個別に指定
(1-3) 計算手法
(1-4) 入力データ（お客様のデータ）について
(1-5) プロダクツ
(1-5-1) 結果ファイル
(1-5-2) PDF形式の図
(1-6) 料金、納期およびご発注手順
(1-7) 個人情報、お客様のデータに関する情報保護
(2章) プロダクツの詳細及びその使用例
(2-1) 結果ファイル
(2-1-1) 結果ファイルのフォーマット（形式）
(2-1-2) 結果ファイルに記述する計算結果の内容
(2-1-2-1) 周波数 (Frequency)
(2-1-2-2) 周期 (Period)
(2-1-2-3) PSD (PSD)
(2-1-2-4) PSDの信頼区間 (Conf Int)
(2-1-2-5) 分散のパーセンテージ (% of Var)
(2-1-2-6) 振幅 (Amplitude)
(2-1-2-7) 位相 (Phase)
(2-1-3) 結果ファイルに書き出された情報の利用方法及び使用例
(2-1-3-1) 結果ファイルの値を用いて独自の図を作成したい場合
(2-1-3-2) PSD及びPSDの信頼区間の使用方法
(2-1-3-3) 特定の周波数での変動の巾（大きさ）を知りたい場合
(ケース1) 信号は振幅が一定の単一の周波数の三角関数で表される場合
(ケース2) 信号は振幅が一定の異なった周波数の三角関数を足し合わせたもので表される場合
(ケース3) 信号は単一の周波数の三角関数だが、振幅が時間とともに変動する場合
(ケース3-1) 信号の振幅の変動そのものが三角関数の形の場合
(例１) 信号は三角関数で周波数はf0。信号の振幅は周波数f1の三角関数の形で変動
(例２) 信号は三角関数で周波数はf0。信号の振幅は定数に周波数f1の三角関数を足し合わせた形で変動
(ケース3-2) 信号の振幅の変動そのものは三角関数ではない場合
(ケース4) 信号は周期的だが、三角関数の形ではない場合
(2-1-3-4) 特定の周波数域内の変動が全体の変動と比べてどの程度強いのかを知りたい場合
(2-1-3-5) 簡易デジタルフィルター（PD001Aのみ適用）
(2-1-3-6)データ中の値の変動の振幅を求める他の方法
(2-2) 図
(3章) PD001シリーズ用のデータファイルの作成手順例
(4章) 各種指定項目の設定について
(4-1) トレンド除去；有無 無指定時は有
(4-1-1) トレンドとは？ 除去の目的は？
(4-1-2) トレンド除去の例
(4-1-3) トレンド除去で問題が発生する例
(4-2) テューキー窓関数のテーパー比；%で表したテーパー比 無指定時は10%
(4-2-1) 窓関数を適用する理由
(4-2-2) 窓関数の適用とは
(4-2-3) ハニング窓関数；使用すると問題が生じる場合について
(4-2-4) 本小額定型計算業務 PD001Aでハニング窓関数を適用したPSDのみではなく、窓関数非適用及びテューキー窓関数を適用したPSDも計算する理由
(4-2-5) ハニング窓関数によるデータ両端近くの減衰を少なくする方法
(4-2-6) 窓関数が持つFDSに似た効果について
(4-2-7) IFDSは必ずしもPSDを平滑化しない
(4-2-8) 窓関数適用によるPSDや振幅スペクトル減衰に対する補正
(4-2-9) 窓関数適用時の補正の効果
(4-2-10) テューキー窓関数のテーパー比がPSDに与える影響
(4-3) 周波数領域での平滑化（FDS）ビン巾； 1、3、5、7等奇数 無指定時は無し（1）、3及び7
(4-3-1) PSDに対するFDS
(4-3-2) 振幅スペクトルに対するFDS
(4-3-3) FDSを適用した場合の周波数解像度
(4-3-4) FDSに代わる他の平滑化法
補足１ コンピュータを用いて計算をする際に生じる誤差について
補足２ パワースペクトル密度関数のスペクトル漏れと窓関数の関係について
補足３ データ長が短いと単一のピークが現れ、長いとツインピークが現れる理由
補足４ S1のトレンド除去により付加される直線成分のPSDの悪影響に対するS1とSRの周波数の関係
(2-2) 図
本小額定型計算業務 PD001AではプロダクツとしてPSDの図をPDF形式で提供致します。図の形式は以下のようになります。なお、PD001Bでは図の提供はいたしません。
・縦（垂直）軸は対数スケール
・横（水平）軸は均等スケール
・横軸の値は周波数
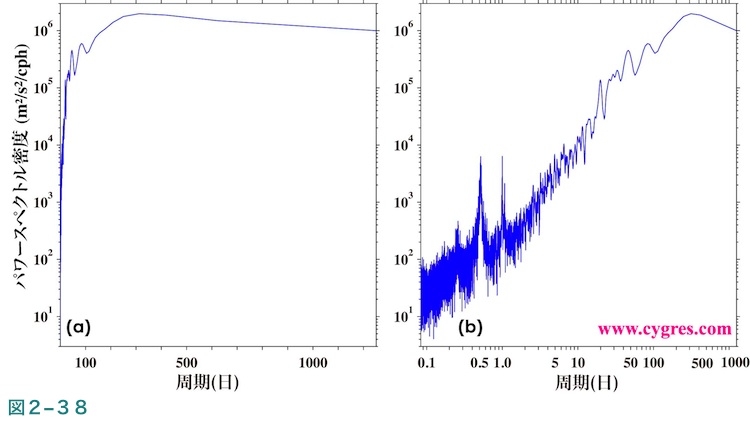
図2-37(a)は上の形式の図の例で、この図のPSDそのものは横軸にも対数スケールを採用した図1-1(b)と同じです。前述したようにPSDは一定の周波数間隔で計算されますので、PSDが計算された点の水平間隔は図2-37(a)では一定になっています。一般にPSDの値はその範囲が広いので縦軸には対数スケールを用いますが、その結果として視覚的に比較的小さい値の部分が拡大され、大きい値の部分が圧縮されます。図2-37(a)中の赤色の水平の実線はピークDのPSDの値を、赤色の水平の破線はPSDの最大値を示します。視覚的にはこの２つの線の高さの差は図全体の高さの半分以下ですが、値そのものは破線のほうが実線の値の約313倍になっています。従って図2-37(b)に示すように、もし縦軸にも均等スケールを採用するとピークDも含めすべてのピークが見えなくなってしまいます。図2-37(b)の下側の枠は赤くなっていますが、この線が図2-37(a)の中央付近にある赤色の実線に相当します。
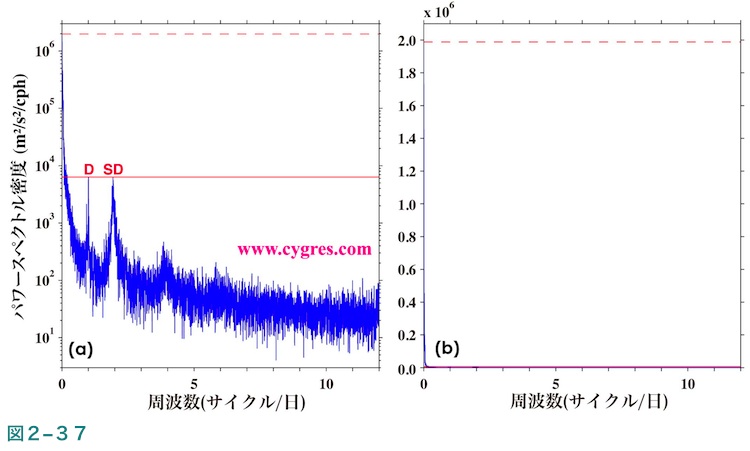横軸の値として周波数ではなく周期を使うことも可能ですが、その場合に横軸に均等スケールを採用すると図2-38(a)に示すようにやや使いにくい図になることがあります。ここで示すPSDの場合、周期100日未満のビンは14988あるのに対し、周期100日以上のビンは13しかありません。従って周期を横軸に使う場合は図2-37(b)に示すように横軸にも対数スケールを採用したほうがよい場合があります。
現在はPD001Aでご提供する図は図2-37(a)のように縦軸は対数スケール、横軸は均等スケールで横軸の値は周波数として定型化させて頂いていますが、お客様からのご要望が多い場合は将来は図についても一部の仕様は選択可能と致します。なお、当事業所では各種仕様に基づく作図もお承りますので、現在PD001Aでご提供の図とは異なる仕様の図が必要な場合はお問い合わせください。お見積もりは無料です。ただし、一般的には作図処理は手作業の部分が多いため、本小額定型計算業務 PD001Aの費用より相当高額になる可能性もある点についてはあらかじめご了承お願い致します。
(3章) PD001シリーズ用のデータファイルの作成手順例
ここではマイクロソフト社のエクセルを用いてPD001シリーズ用のデータファイルを作成する手順を示します。なお、データ数の異なる複数のセットのデータのPSDの計算を同時に発注される場合は、データ数の異なるものが同じファイル内に混在しないようにファイルを分けて頂きますようお願い致します。具体的には例えばデータセット１、２及び３があり、データ数がそれぞれ20、30及び20であったとすると、データセット１及び３は同じファイルにし、セータセット２は別のファイルに分離するか、あるいはデータセット毎に１ファイル、計３ファイルを作成して頂きますようお願い致します。
なお、PD001シリーズでお取り扱いできるデータファイルは半角アスキーコードで数値及び数値間の区切りとして半角のスペースまたは半角のコンマのみを含むファイルです。バイナリーのデータファイル、アスキーコードでも全角の数値やスペース、コンマを含む場合や半角の数字のみでも複雑な順序で記録されているような場合は当事業所で変換用のプログラムを作成して処理することは可能ですが、その場合は別途処理料金が発生致します。
手順１：目的とするファイルをエクセルで開きます。
手順２：該当ファイル中の目的とするセルを選択します。
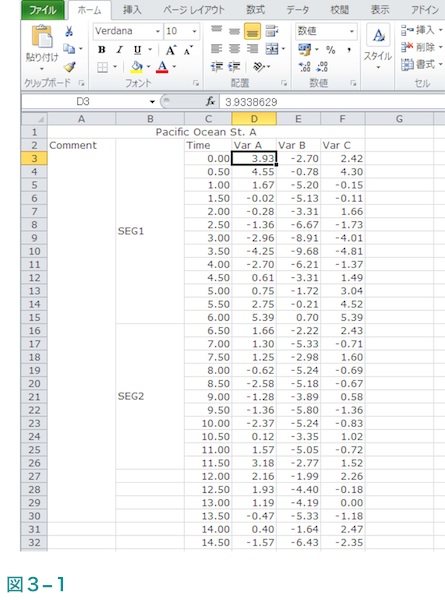
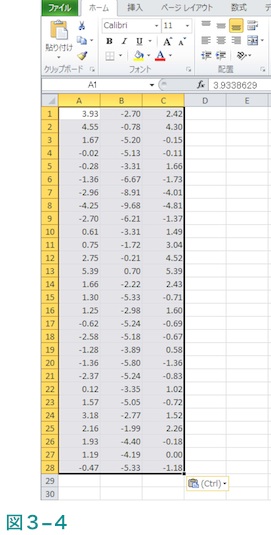
ここでは図3-1で示す例で”Var A”及び”Var C”の3行目から30行目迄のデータよりPSDを計算したいとします。まず、この範囲内の右上端のセルを左クリックします。
次にマウスの左ボタンを押したままカーソルを必要な範囲内の左下端までドラッグし、ボタンを離します。
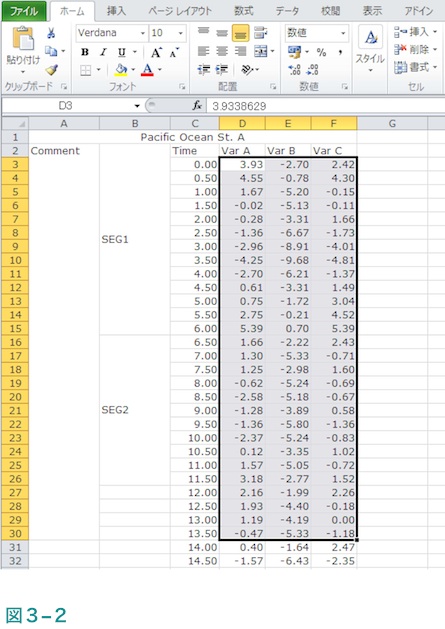
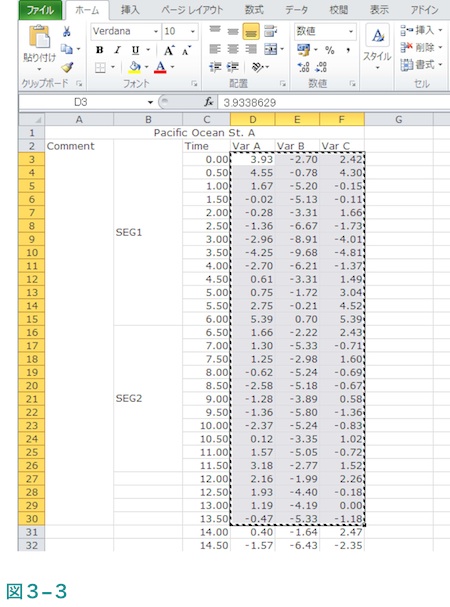
これで必要な範囲は選択されたことになります。図3-2で示す範囲内にはここでは不要な”Var B”のデータ（E列）も入っていますが、それについては計算対象が作成したデータファイルの１列目と３列目であるという連絡を頂ける限り削除されなくても結構です。なお、ここで選択範囲内にあるのは半角の数字のみで数字以外のものや全角の数字は含まれていないことをご確認お願い致します。
手順３：選択した範囲のセルをコピーします。
これは普通のコピー＋ペーストを行う際のコピーです。
手順４：新規に別のワークシートを作成します。
手順５：新規に作成したワークシートに先ほどコピーした内容をペーストします。
手順６（最終）：このワークシートをcsv形式で保存します。
ファイルメニューで”名前を付けて保存”を選び、そこで表示されたダイアログボックスにある”ファイルの種類”の中から”CSV（カンマ区切り）”を選択した後保存します。
なお、この保存されたファイルをマイクロソフト社のメモ帳で開くと図3-5のようになります。この図ではコンマの水平位置が縦方向では揃っていませんが、それは問題ではありません。
(4章) 各種指定項目の設定について
本章では小額定型計算業務 PD001シリーズでお客様にご指定頂く各種設定についての解説を記述しています。この章では他章に比べ数式等をやや多用致しますが、本業務のご発注を検討されている場合で本章の内容の説明が必要な場合はお問い合わせください。
(4-1) トレンド除去；有無 無指定時は有
一般的にはPSDを計算する前にデータからのトレンド除去を行います。ここでは最初に本小額定型計算業務PD001シリーズでおこなうトレンド除去がどういうものであるかを記述し、その後にトレンド除去を行うと問題が発生する稀なケースについて記述します。
(4-1-1) トレンドとは？ 除去の目的は？
PD001シリーズにおいてトレンドというのはデータの値を最小自乗法という方法によって直線で近似したもので、トレンド除去というのはデータの各値からこの直線で近似した値を差し引く操作です。トレンド除去の目的はデータに含まれる非常に低い周波数（０から最初のビンの周波数）の変動を除くことにより、主に周波数の低い部分のPSDの計算精度の向上を計ることにあります。なお、実際に直線で表されるような変動があると、後で示すように全周波数域でPSDの値が少し増加します。実際の計測データでは計測機器周辺の温度等の環境変化やセンサーや計測回路自体の特性の経時変化などにより直線で近似できるような緩やかな変動（ドリフト）が含まれることがあります。
なお、PD001シリーズにおいて行うような方法でデータからトレンドを除去すると、データの平均値（DC（直流）成分と称される場合もあります）も自動的に除去されます。その結果、周波数ゼロのビンのPSDは計算上の数値誤差範囲内でゼロになります。平均値は時間変化をしない定数ですので、本来は平均値の除去は周波数ゼロのビン以外のビンのPSDの値には影響するべきではないのですが、平均値がゼロでない場合にFDSや窓関数を適用すると他の周波数のビンのPSDにも悪影響を与えることが考えられます。
(4-1-2) トレンド除去の例
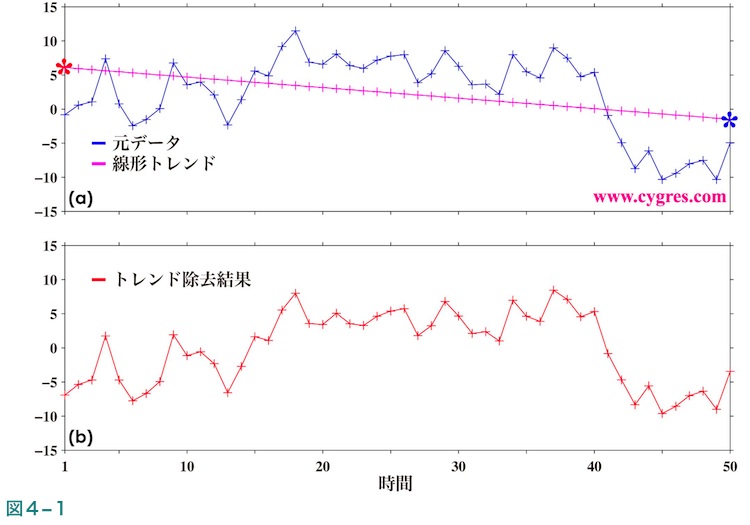
図4-1(a)の青色の線はここで使用するデータの時系列で、この図中のプラス記号（+）は実際のデータの時間（水平位置）及び値（垂直位置）を示します。トレンド除去作業で最初にすることはこのデータを直線で近似することですが、これは下の式中の左辺の誤差を最小にするような傾きと切片を最小自乗法で計算することになります。
ここでNはデータの数、tmはm番目のデータの時間（図中プラス記号各点の水平位置）でV(tm)はデータの値（図中プラス記号各点の垂直位置）です。ここで、傾きとは図中の値を使用すると、
で、切片とは紫色の線が時間ゼロの点（図の左端より１ポイント左）で持つ値です。傾きと切片を計算した後はこれらの値を用いてデータの直線近似値を式、傾きx tm + 切片、よりデータのある各時間tmで計算しますが、これが図中の紫色の線で示すトレンドとなります。最後にこの直線近似値をデータから差し引きます。図4-1(b)はトレンドが除去されたデータを示します。
(4-1-3) トレンド除去で問題が発生する例
PD001シリーズで行うような直線近似によるトレンド除去は通常は問題を起こさないのですが、非常に強い信号と非常に弱い信号が混在している場合で、弱い方の信号のPSDを精確に得たい場合などには問題となることがあります。ただし、通常はデータの有効な桁数の限界やセンサーの精度の限界といったデータの精度自体の限界があるのが普通ですので、ここで記述するような問題が生じる程の弱い信号は存在できない場合も多々あります。
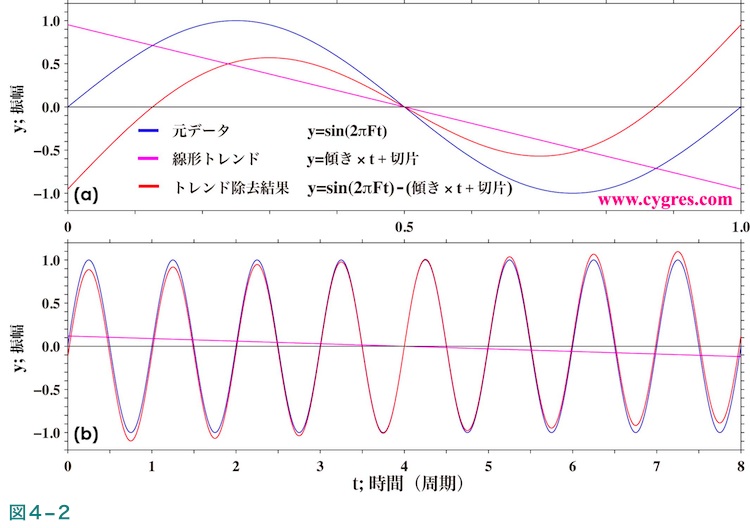
図4-2(a)の青色の線は図2-4(a)で使用した単純な三角関数の最初の１周期+１ポイントの部分を示します。ここで１ポイント余分に足しているのは、このデータは一定の時間間隔の値ですので、この図のように最初の値の時間をゼロとして開始すると、最初の周期の最後の点は値が３回目にゼロになる点の一つ前になるためです。この図では最初の点、中央の点と最後の点の値はゼロになっています。ここで、この青色の線で示されるデータの直線近似がどうなるかということを単純に考えると、図中の縦軸の値がゼロの位置にある黒の直線で示される線、すなわちトレンドはない（傾きも切片もゼロ）と考えてしまいます。
しかし、実際に式(13)を使用して計算しますと上の単純な考えは誤りで、トレンドは図中の紫色の線で表されるものになり、図中の赤色の線がトレンド除去の結果になります。図4-2(b)はデータ長を8周期分（図2-4(b)で短い縦の青線で示したデータ長Aに相当）にした場合の結果ですが、この図で示すようにデータをかなり長くしても三角関数のトレンドはゼロになりません。
このように、ここで記述するトレンド除去の問題は純粋な三角関数から直線近似によるトレンドを除去すると、元の純粋な三角関数に元々は存在しなかった直線の傾きを実際には与えてしまうという事実によります。なお、ここで三角関数を例に出したのは、式(3)で示すようにPD001シリーズやその他の一般的なスペクトル解析で行うようなPSDの計算は元のデータが色々な周波数の純粋な三角関数の和として表すことができることを前提としているからです。
三角関数の直線近似の傾きは、データのサンプリング間隔が微小であるとして式(13)の和の部分を積分に置き換えて計算すると
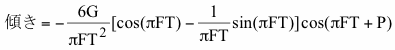
のようになります。ここでGは三角関数の振幅、Fは周波数、Pは位相で、データとしての三角関数は時間0で開始し、必ずしも特定の周期には一致しない任意の値Tで終了するとしています。なお、この式を得るための詳細は長い代数の表示が必要になるので割愛します。図4-2やこの文書中の他の例のように上の式中のP（位相）をゼロにすると、上の式は
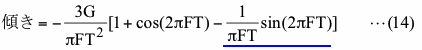
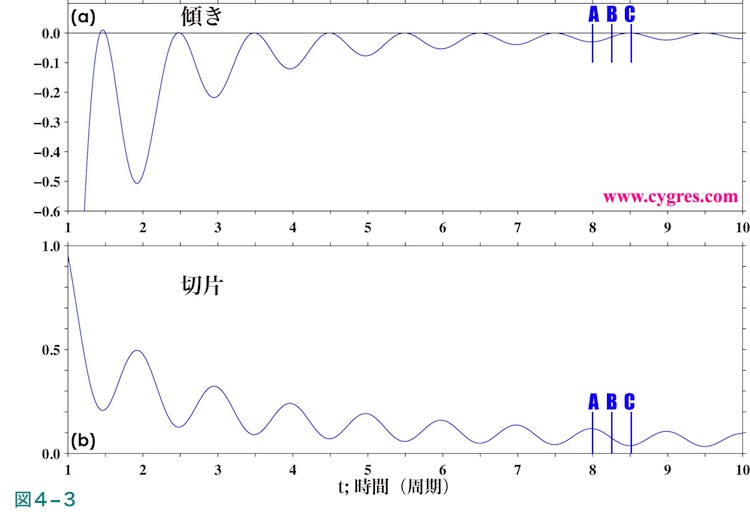
となります。図4-3(a)は上の式でG（振幅）を1.0にしたときに、T（データ長）が長くなるにつれ傾きの値がどのように変化するかを示します。この図の横軸の単位は三角関数の周期（=1/F）で、短い青色の縦の実線で示したデータ長A、B及びCは図2-4(b)で示したデータ長と同じです。なお、データの開始時間を三角関数の半周期分ずらすと、傾きは図の0の値の高さに引いた水平の黒の実線を基準軸として上下に反転させたものになります。
上式及び図4-3(a)により、時間0で開始した三角関数を直線近似すると、傾きはほぼ常に負の値をとり、データ長が三角関数の各周期より半周期分長い場合又はデータ長が非常に長い（数学的には無限大）場合のみゼロとなることがわかります。また、上式により傾きはG（三角関数の振幅）が大きくなるにつれ大きくなり、F（三角関数の周波数）またはT（データ長）が増加するにつれ小さくなることがわかります。Tが固定されている場合は、Fが大きくなるにつれ傾きは小さくなります。
以上により直線近似法を用いて本来はトレンドはないと考えられる純粋な三角関数からトレンドを除去しようとすると逆に直線成分を与えてしまう結果になります。ここでさらに皮肉な点は、前述したようにPSDの計算結果は周波数一致が成立した場合に最も精確になるのですが、逆に付加する直線成分の傾きは周波数一致が成立するデータ長（例えば図4-3(a)のデータ長A）で大きくなる点です。なお、以下では純粋な三角関数を信号と称します。
純粋な三角関数に直線成分を与えてしまうと本来の信号によるPSDに直線成分のPSDが加わってしまうという悪影響が発生します。T（データ長）が図4-3のAの場合は信号に対し周波数一致が成立していますので、この信号のみを含むデータのPSDは図2-5(a)で示したように信号ビンのみ値を持ち、他のビンの値はすべてゼロになります。ここで、式(14)で示す直線成分がデータに加わった場合（厳密には式(14)で示す直線近似値を引きますので、正負符号は反転します）はその直線成分のみによるPSDはG（振幅）の値を1.0として、データ長がAの場合はk番目のビンで
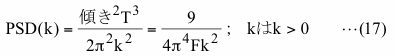
のようになります。なお、0番目のビンは周波数ゼロ（平均値）のビンでデータの値の変動には寄与しないビンです。この式により直線成分のみによるPSDは信号の周波数が低くなる（Fが小さくなる）につれ増加することがわかります。なお、周波数一致が成立している場合の信号に直線成分が加わったデータのPSDは信号のPSDにこの直線成分のPSDを加えたものになります。
式(17)で表される直線成分のPSDを対数スケールで描画すると一定の傾き、-2.0、を持った直線になります。具体的には式(17)の両側の対数をとると下式のようになります。
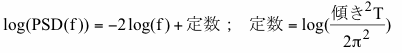
ここでk番目のビンの周波数fはk/Tです。上の式は傾きが-2.0の直線の方程式、y= -2x + 定数、と同じ形です。
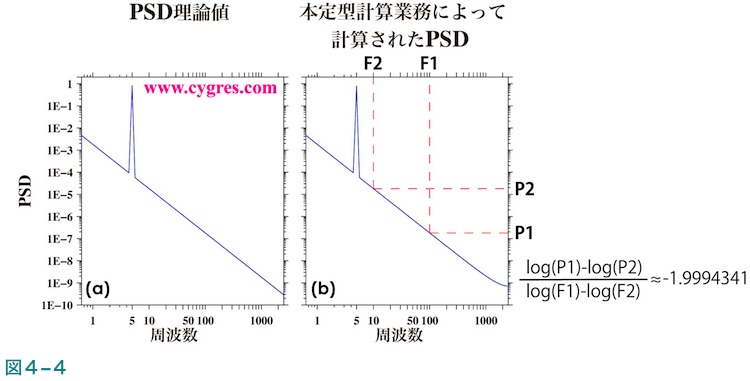
この式の結果に信号のPSDを付加したものを図4-4(a)に示します。これに対し、信号のみを含んだデータに実際にトレンド除去を適用した後PD001Aを使用して計算したPSDを図4-4(b)に示します。なお、窓関数は適用していません。図4-4(b)の直線部分より計算した傾きは約-1.9994341で、上の式の値、-2.0にほぼ一致します。なお、図4-4で表示しているのは周波数ゼロのビンの次のビンからで、周波数ゼロのビンの値はデータの値の変動には無関係ですし、0の対数値は負の無限大となって対数スケールの図では表示できないので図4-4には表示していません。
周波数一致が成立しない場合はここで示したような２つのPSDの単純な和にはならず、やや複雑になります。また周波数一致が成立しない場合は全周波数領域で信号部分からのスペクトル漏れが起きるため、次に示すように直線成分付加の影響は目立たなくなる可能性もあります。
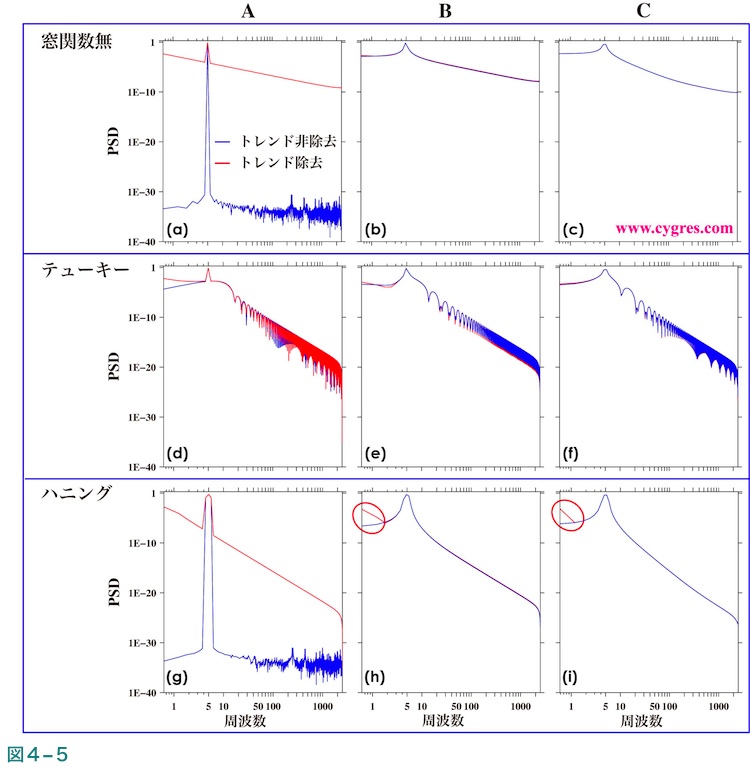
図4-5(a)は上の例と同じ純粋な三角関数の信号のみを含むデータを用い、データ長がAで窓関数を適用せずに計算したPSDで、赤線がトレンド除去を適用した場合を、青線がトレンド除去を適用しなかった場合を示します。なお、図4-4と同様に図4-5で表示しているのは周波数ゼロのビンの次のビンからで、周波数ゼロのビンの値は表示していません。ここでこの図の赤線は図4-4(b)の青線と、この図の青線は図2-8(a)の紫線と図の縦軸の表示範囲が異なること以外は同じです。なお、上の例と同様にトレンド除去を適用しないとデータは純粋な三角関数しか含みませんが、トレンド除去を適用すると逆にデータ中の純粋な三角関数に直線成分が付加されます。トレンド除去の悪影響はこの図では明白ですが、信号のピーク自体が不明確になるようなことはありません。図4-5(b)及び(c)はデータ長をB及びCに変更した以外は図4-5(a)と同じ条件で計算したPSDです。これらの図にはトレンド除去を適用しなかった場合の青線しかないように見えますが、実際には赤線の上に青線が被さっています。これらの図により、このように周波数一致が成立しないケースでは信号からのスペクトル漏れの影響がトレンド除去を行った場合の悪影響より遥かに大きいため、トレンド除去を行っても実質の問題は生じない場合があります。
図4-5(d)、(e)及び(f)はPSDを計算する前にテーパー比10%のテューキー窓関数を適用した以外は図4-5(a)、(b)及び(c)と同じです。データ長がA又はBの場合はトレンド除去の有無の差は視認できる程度にはあることがわかりますが、窓関数が持つIFDSにより生じる丘状のものの影響も大きいためあまり目立ちません。データ長がCの場合（図4-5(f)）は窓関数非適用の場合（図4-5(c)）と同様に信号からのスペクトル漏れの影響が大きいため、トレンド除去の有無の差は視認できません。図4-5(g)、(h)及び(i)はPSDを計算する前にハニング窓関数を適用した場合の結果ですが、トレンド除去の悪影響もスペクトル漏れの影響も他に比べれば小さくなっています。以上により、一般的には信号が周波数の比較的低い純粋な三角関数で周波数一致が成立しない場合は、信号からのスペクトル漏れの為にトレンド除去を行ってもその悪影響が目立つような事はあまりありません。ただし後で示すように信号の周波数が比較的高い場合は例え信号からのスペクトル漏れがあってもトレンド除去の悪影響が視認できるほど大きくなることがあります。
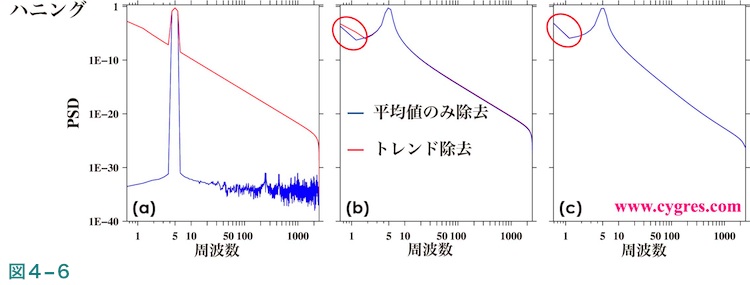
データ長がB又はCで、ハニング窓関数を適用した場合に最も低い周波数部分で生じる差異（図4-5(h)及び(i)中の赤丸部分）の原因はやや複雑です。PSDの計算前にデータのトレンド除去は行わずに平均値の除去のみを行った計算結果を図4-6(a)、(b)及び(c)の青線に、図4-5の赤線と同様にデータのトレンド除去を行った計算結果を赤線に示します。図4-6においては、データ長がB又はCの場合は周波数ゼロの次に周波数の低いビン（図の左端上のビン）のPSDの値はそれより一点右のPSDの値より大きくなっています。これは周波数ゼロのビンのPSDの値（図では表示していません）をゼロにする平均値除去の影響及びハニング窓関数が持つIFDSの効果のためです。(4-2-7)で記述するようにハニング窓関数のIFDSは必ずしもPSDを平滑化するとは限りません。前述したようにトレンド除去を行うとデータから平均値も除去されるため、図中の赤線でも同様に周波数ゼロの次に周波数の低いビンの値が大きくなっています。なお、もしここでこの結果にFDSを適用すると図の左端上のビンのPSDの値は周波数ゼロのビンの値がゼロのため、図で表示した結果とは逆にかなり小さくなります。テーパー比10%のテューキー窓関数を適用した場合にはこのような差異は視認できませんが、これはテューキー窓関数のIFDSとハニング窓関数のIFDSが異なるためです。
一般的にはデータからの平均値除去は、トレンド除去を行わないケースでも最低限行わなければならない事と考えられているようです。データの平均値がゼロでない場合は周波数ゼロのビンのPSDの値がゼロでない値になり、そのため窓関数やFDSを適用するとその影響が他の低い周波数のビンのPSDの値にも波及してきます。これは上で記述したように平均値を除去すると周波数のゼロのビンのPSDの隣のビンのPSDの値が大きくなるという事とは矛盾しているようですが、このような結果になった原因は窓関数が持つIFDSの効果のためであり、一般的には必ずしもこのようになるとは限りません。また、通常のデータはここで示したデータと異なりいろいろな周波数の信号やノイズが含まれているので、ここで示したような平均値除去の問題が生じる可能性はあまりないと思われます。いずれにしろ、PD001Aでは窓関数に関しては非適用の結果も提供致しますので、特定のビンのPSDの値が非常に重要な場合は複数の結果を比較されることをお薦め致します。
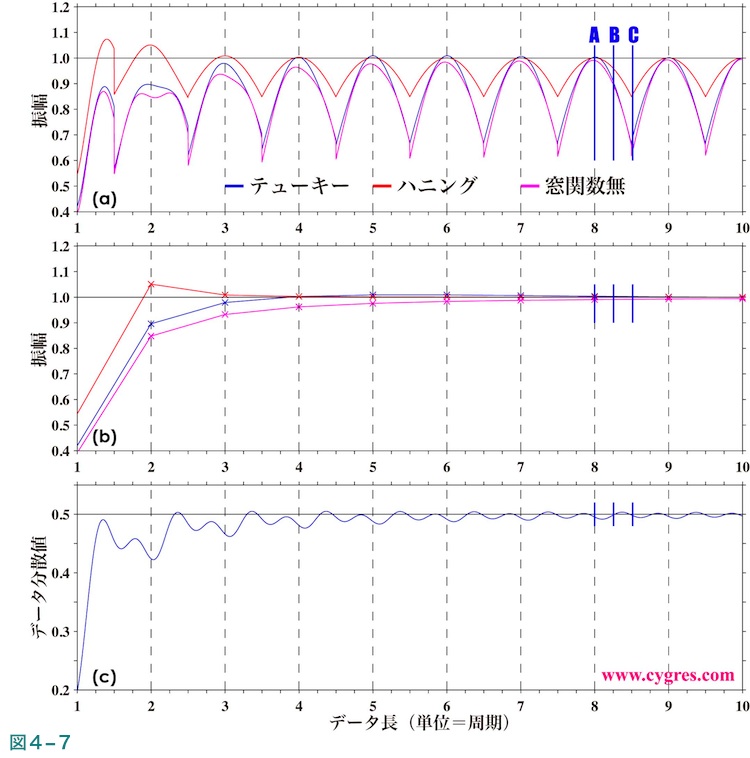
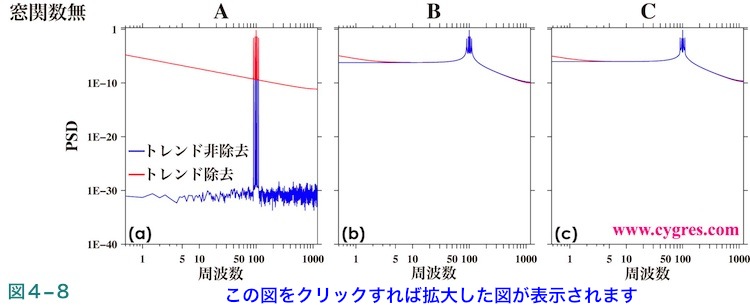
図4-7(a)はトレンド除去を適用した場合に信号ビンの振幅がデータが増えるにつれどのように変化するかを示します。この図とトレンド除去を適用しなかった場合の結果である図2-4(b)と比較すると、トレンド除去を適用した場合は信号ビンの振幅がデータが増えるにつれ実際の信号の振幅に近づくペースがより緩やかになっていることがわかります。これについては周波数一致が成立している場合のみ抽出して描画した図4-7(b)と図2-4(c)とを比較するとより明白になります。図4-7(c)は図2-4(d)と同様にデータの分散を示した図ですが、データ長が2.0以下ではかなり大きな変動をしています。以上のように細かな差がトレンド除去適用の有無で生じますが、データ長が信号の数周期以上あればトレンド除去適用の有無が信号ビンの振幅に与える影響は比較的小さいと考えられます。
図4-8は異なった周波数の複数の信号がある場合のPSDを示します。ここで使用したデータは図2-19(a)の最上段のSで、図4-8(a)の青線は図2-22の赤線と同じです。このように信号が複数混在する場合にも上述したような問題は発生します。なお、データ長がB（図4-8(b)）又はC（同(c)）の場合は信号からのスペクトル漏れが発生していますが、図4-5等で示した結果と異なり、低い周波数域ではトレンド除去の適用の有無の差が視認できるほど生じています。これはこういった周波数域の周波数と信号群の周波数の差が大きいので、信号からのスペクトル漏れの影響はトレンド除去によって付加された直線成分によるPSDより小さくなっているためです。
では、次に非常に強い信号と非常に弱い信号が混在している場合にどうなるかを示します。ここでは非常に強い信号は単一の周波数の純粋な三角関数の信号で、以下ではS1と称します。非常に弱い信号の方は図1-1(a)で示したデータの一部を使い、これを以下ではSRと称します。図4-9(a)にSRの時系列図を、同(b)にトレンドを除去しテューキー窓関数を適用した場合のSRのPSDを示します。このPSDにはS2とS3という比較的目立つピークがありますので、これを以下では目印とします。なお、この２つのピークが表す変動は元のデータの潮汐成分で、データの開始時から終了時まで安定して存在しているため(4-2-3)で記述するような窓関数による問題が発生しにくいので好都合です。なお、図4-9(a)の横軸で使用している単位はS1の周期で図1-1(a)のものとは異なります。
ここでは最初にS1の周波数が比較的低い場合を考えます。図4-9(c)はS1とSRを足し合わせたデータですが、SRの分散はS1の分散の1万分の1（0.0001）に設定していますので、SRを視認することはできません。なお、振幅比では大雑把にSRはS1の約300万分の1程度です。図中の赤色の縦の実線で示したデータ長AはS1について周波数一致が成立しているデータ長で、データ長CはS1の周波数がS1の信号ビンの周波数から最も離れている場合です。これらのデータ長は図2-4で使用したものと同じですが、図2-4中にあるデータ長Bの結果はここでは省略します。なお、以下ではS1とSRを足し合わせたものをテストデータと称します。
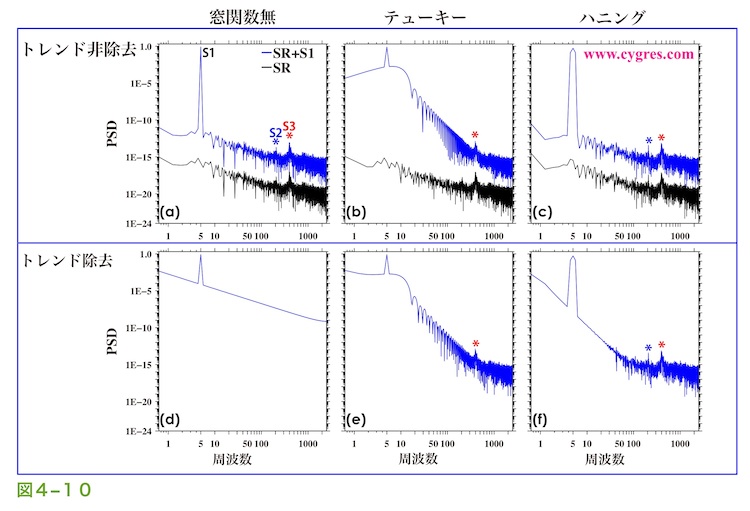
図4-10上段の３図の青線はデータ長がAでトレンド除去を適用しなかった場合のテストデータのPSDを、黒線は同様にして計算したSRのPSDを示します。図中の青の米記号はS2を、赤の米記号はS3を示します。なお、SRのPSD（黒線）は図を見やすくするために下方に移動させています。データ長Aは前述したようにS1について周波数一致が成立している場合で、S1からのスペクトル漏れはないので、窓関数のIFDSの影響がはっきりと現れます。ただし、現実のデータを扱う場合はデータ中に周波数の異なった複数の信号やノイズが含まれるのが普通で、図4-10のように周波数一致を成立させるのは困難です。従ってここで示す結果はやや非現実的なものになります。図4-10(a)よりトレンド除去も窓関数も適用しなかった場合はS1の影響はS1の信号ビンにのみ限定され、S1の信号ビン以外のビンではSRのPSDがそのまま現れます。しかし、テューキー窓関数を適用すると、窓関数のもつIFDSの効果によってS1の影響が広がるため、図4-10(b)で示されるようにS1の信号ビン周辺のかなりの周波数域でSRのPSDが不明確になります。ハニング窓関数を適用した場合も窓関数の持つIFDSの効果によってS1の影響が広がりますが、その影響は(4-2-6)で記述するように信号ビンの両隣のビンに限られますので、信号ビンを中心とした3つのビン以外では図4-10(c)に示すようにSRのPSDがそのまま現れます。
図4-10下段にトレンド除去を適用した結果を示します。図4-10(d)より窓関数を適用しなかった場合は図4-4(b)に示すようなトレンド除去によって付加されたS1による直線成分のPSDのため、SRのPSDは全く視認できません。ここで、SRのPSDが視認できない理由はトレンド除去によって付加された直線成分によるPSDの下にSRのPSDが埋もれたからではありません。データ長がAの場合のテストデータのPSDは付加された直線成分も含むS1のPSDとSRのPSDを単純に足し合わせたものに近いのですが、付加された直線成分のPSDがSRのPSDに比べ相当大きいため、両者を足し合わせてもその違いが目で見える程に変わらないためです。具体的にはS3の場合はその周波数での付加された直線成分によるPSDはSRのPSDの17000倍もあるので、その２つの値を足し合わせても付加された直線成分によるPSDのみの値とほとんど変わりません。
図4-10(b)と(e)を比較すると、テューキー窓関数を適用した場合はIFDSの効果が非常に強いためトレンド除去適用の有無による差はあまりないことがわかります。一番分かりやすい差はS1より左の低周波数域で生じています。ハニング窓関数を適用した場合についてはトレンドを除去した場合は図4-10(f)の中央やや右あたりから図の左端まで付加された直線成分のPSDが顕著に現れ、SRはほとんど視認できませんが、図の右半分ではSRのPSDが明確に現れます。
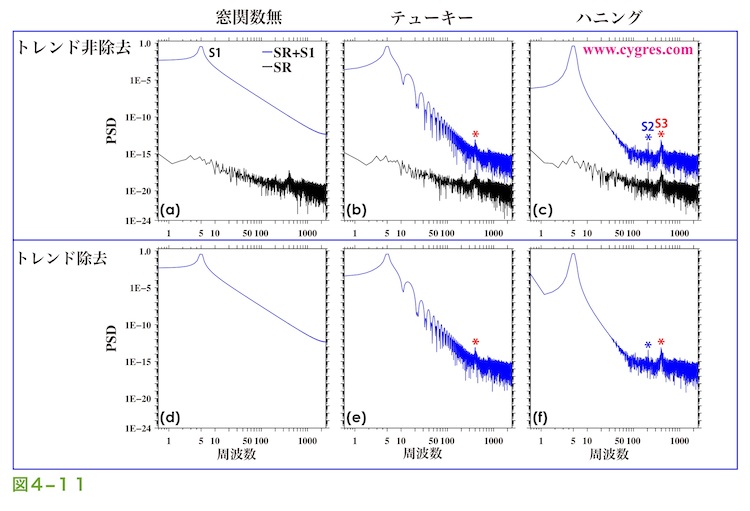
図4-11はS1からのスペクトル漏れがある場合の例としてデータ長がCの場合のPSDを示します。実際のデータを扱う場合は周波数一致を成立させるのは難しい場合が多いので、図4-10より図4-11のほうが現実的です。窓関数を適用しなかった場合（図4-11(a)及び(d)）はS1からのスペクトル漏れの影響が非常に強いためトレンド除去の有無には無関係にSRは全く視認できません。窓関数を適用した場合はS1からのスペクトル漏れの影響は多少は押さえられますが、窓関数のIFDSの効果もあり、結果としてトレンド除去の有無の差は窓関数非適用の場合と同じくほとんどありません。ただし、これらの結論はS1の周波数が比較的低い場合で、S1の周波数が比較的高い場合は次に記述するように少々変わってきます。
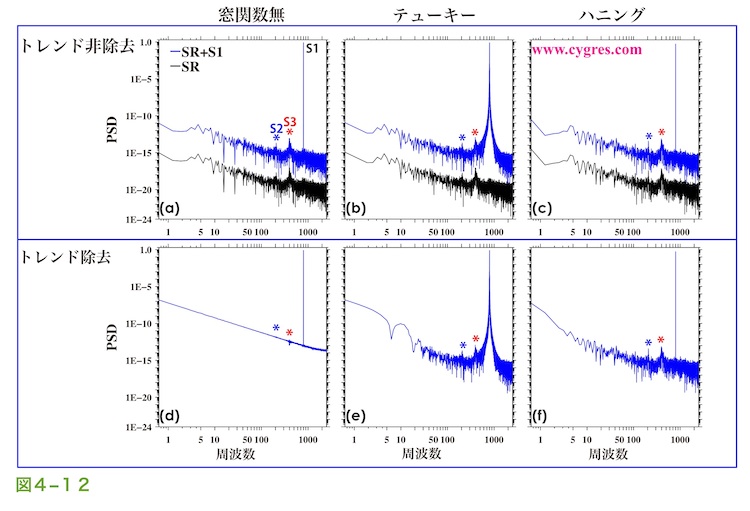
ここで、他の条件は一切変えずにS1の周波数のみを高くしてみます。図4-12は図4-10に対応する図で、周波数一致が成立する場合のPSDです。図4-10で示した結果と同様に、この場合でもトレンド除去も窓関数も適用しない場合はS1の影響はS1の信号ビンのみに限定されます。図4-12の各図と図4-10の各図を比較するとS1が巾の狭いよりシャープなピークになっているように見えますが、これは横軸にも対数スケール採用したために生じる見かけ上の効果です。同様に図4-12(b)と図4-10(b)の比較より、IFDSによるS1の影響の広がり方がこの例ではかなり狭くなっているように見えますが、これも横軸に対数スケール採用したために生じた見かけ上の効果で、IFDSによる影響の広がり方はその大きさも含めS1の周波数には依存しません。図4-12(d)と図4-10(d)の比較より、トレンド除去を適用した場合の直線成分付加による悪影響はこの例ではかなり小さくなっていることがわかります。これは式(17)で示すように付加された直線成分のPSDの大きさはS1の周波数に反比例するからですが、この点についての詳細は補足４に記述します。
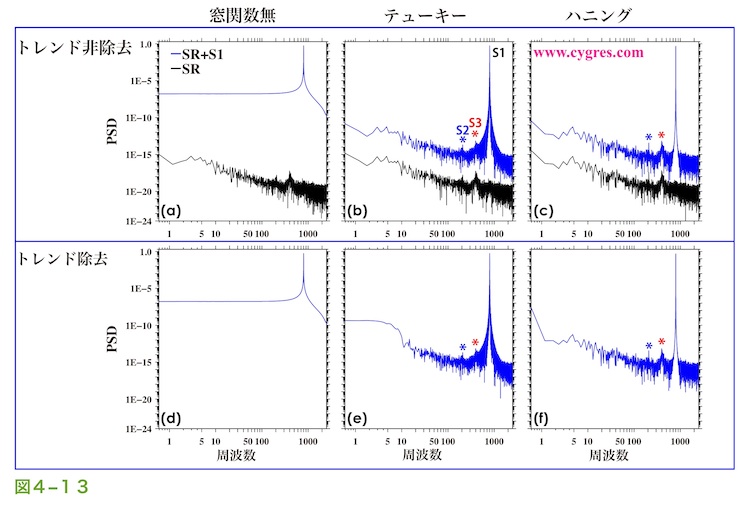
図4-13はデータ長をCにした場合のPSDで図4-11に対応する図です。窓関数を適用しなかった場合はSRのPSDはトレンド除去の有無には関係なく視認できません。窓関数を適用した場合はトレンド除去の有無の差が図4-11に比べかなり明らかになり、トレンド除去を行わないほうがSRがより明白になります。トレンド除去の有無の違いは低周波数域では明らかになりますが、これはトレンド除去を適用した場合の直線成分付加による悪影響は上の式や図4-4に示すように周波数が低くなるにつれ増大するからです。
以上を纏めると、SRの検出が重要であるならばトレンド除去は非適用でハニング窓関数を適用するのが一番良いという事になるようですが、実際にデータに時間とともに直線的な変化をするような成分が含まれる場合はトレンド除去を行わないと同じような問題が発生してしまいます。ここで記述したようなトレンド除去の問題はS1による変動の振幅がSRによる変動の振幅に比べ非常に大きいため、通常は微小なので無視できるようなS1による直線成分付加の悪影響がSRの検出を困難にする程相対的に大きくなっているために生じています。なお、(4-2-3)に記述するようにハニング窓関数は使わない方が良い場合もあります。
非常に強い信号と非常に弱い信号が混在している場合で、両者が存在する周波数帯域が離れている場合は、PSDを計算する前に両者をフィルタで分離した後にそれぞれについてPSDを計算するという方法もあります。当事業所ではそのような計算を行うことも可能ですので、必要であればお問い合わせください。
前ページは左矢印を、次ページは右矢印をクリックしてください
